`A = 0,2+ (0,2)^2 + (0,2)^3 + ... + (0,2)^100`
`A = 1/5 + (1/5)^2 + (1/5)^3 + ... + (1/5)^100`
`5A = 5 . [1/5 + (1/5)^2 + (1/5)^3 ... + (1/5)^100]`
`5A = 1 + 1/5 + (1/5)^2 + ...+ (1/5)^99`
`5A - A = [1 + 1/5 + (1/5)^2 + ... + (1/5)^99]-[1/5 + (1/5)^2 + (1/5)^3 + ... + (1/5)^100]`
`4A = 1 - (1/5)^100`
`A = (1-(1/5)^100)/4`
Vì: `1 - (1/5)^100 < 1` hay `(1-(1/5)^100)/4 < 1/4` nên `A < 1/4`
Vậy: `A <1/4`
`A = 0,2 + (0,2)^2 + ... +(0,2)^100 `
`=> 0,2A = (0,2)^2 + ... + (0,2)^101`
`=> 0,2A - A = ((0,2)^2 + ... + (0,2)^101) -(0,2 + ... +(0,2)^100) `
`=> -0,8A = (0,2)^101 - 0,2`
`=> A = -0,8*((0,2)^101 - 0,2)`
Vì `(0,2)^101 - 0,2>0`
`=> -0,8*((0,2)^101 - 0,2)<0`
Mà `1/4 >0`
`=> -0,8*((0,2)^101 - 0,2)<1/4`
`=> A<1/4`


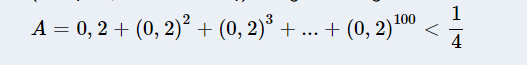













 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ





