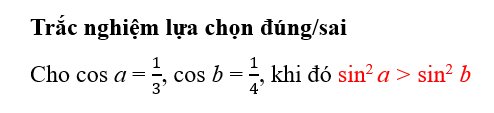Ta có:
\(cos^2a+sin^2a=1\\ =>sin^2a=1-cos^2a=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(cos^2b+sin^2b=1\\ =>sin^2b=1-cos^2b=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
Ta có: `15/16>8/9=>sin^2a<sin^2b`
-> Sai
`cosa = 1/3 `
`=> cos^2 a = 1/9`
`=> sin^2 a = 1 - 1/9 = 8/9`
`cos b = 1/4`
`=> cos^2 b = 1/16`
`=> sin^2 b = 1- 1/16 = 15/16`
Do `1/9 > 1/16 => 8/9 < 15/16`
`=> sin^2 a < sin^2 b`
Vậy ý kiến trên Sai
Ta có:
`\cos(a) = 1/2`
`=> \cos^2(a) = (1/2)^2 = 1/4`
`-> \sin^2(s) = 1 - \cos^2(a) = 1 -1/4=3/4=12/16`
`\cos(b) = 1/4`
`=> \cos^2(b) = (1/4)^2 = 1/16`
`-> \sin^2(b) = 1 - \cos^2(b)= 1 -1/16 = 15/16`
Vì: `12/16 < 15/16` nên `\sin^2(a) < \sin^2(b)`
`->` Sai.
`cos(a) = 1/3 => sin^a = 1 - cos^2a = 8/9`
`cos(b) = 1/4 => sin^2b = 1 - cos^2b = 15/16`
`=> sin^2a < sin^2b`,
`=>` Sai