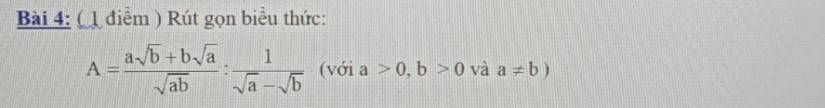\(A=\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\left(a>0;b>0;a\ne b\right)\)
\(=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}\cdot\sqrt{a}-\sqrt{b}\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)
\(=a-b\)
\(A=\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)
\(=a-b\)
\(A=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}\cdot\dfrac{\left(\sqrt{a}-\sqrt[]{b}\right)}{1}\) =\(a-b\) \(DK:a,b\) ≥ 0
\(A=\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\)
\(A=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\sqrt{a}-\sqrt{b}\)
\(A=\left(\sqrt{a}+\sqrt{b}\right).\left(\sqrt{a}-\sqrt{b}\right)\)
\(A=a-b\)