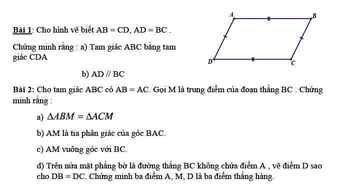
a) Xét △MNP và △QNP có:
MN=NQ
\(\widehat{MNP}=\widehat{QNP}\)
NP là cạnh chung
Khi đó △MNP=△QNP(c.g.c)➜\(\widehat{MPN}=\widehat{QPN}\) (2 cạnh tương ứng) mà tia PN nằm giữa 2 tia PM và PQ➜PN là tia phân giác của\(\widehat{MPQ}\)
b) Vì △MNP=△QNP(Cmt) nên \(\widehat{M}=\widehat{Q}\)(2 góc tương ứng) mà \(\widehat{M}\) vuông ➜\(\widehat{Q}\) vuông hay NQ⊥PQ
c)Gọi giao điểm của NP và MQ là O
Xét △MNO và △QNO có:
MN=NQ
\(\widehat{MNP}=\widehat{QNP}\)\(=\widehat{MNO}=\widehat{QNO}\)
ON là cạnh chung
Khi đó △MNO=△QNO(c.g.c)➜\(\widehat{MON}=\widehat{QON}\)(2 góc tương ứng) (1)
Ta có \(\widehat{MON}+\widehat{QON}=180^0\)(2 góc kề bù) (2)
Từ (1),(2) suy ra \(\widehat{MON}=\widehat{QON}=\dfrac{1}{2}\widehat{MOQ}\)=90 ➜MQ⊥NP






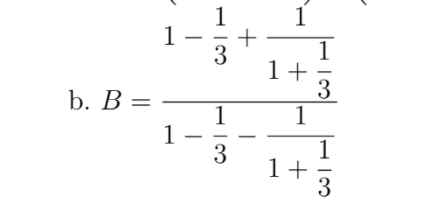 Giúp e vơi ạ!!!
Giúp e vơi ạ!!!