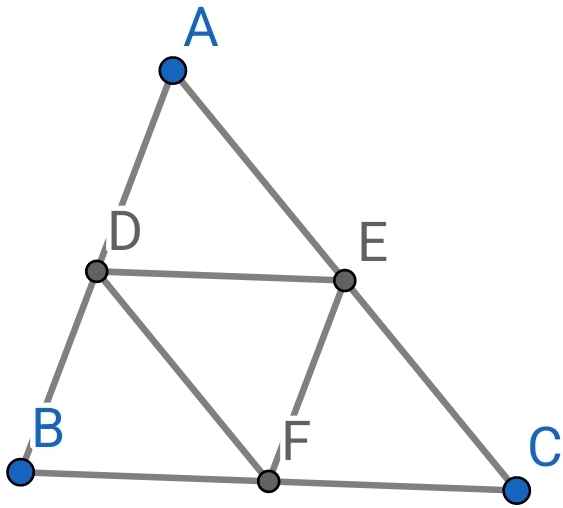
a) Do DE // BC (gt)
⇒ ∠BFD = ∠EDF (so le trong)
Do EF // AB (gt)
⇒ ∠BDF = ∠DFE (so le trong)
Xét ∆BDF và ∆EFD có:
∠BFD = ∠EDF (cmt)
DF là cạnh chung
∠BDF = ∠DFE (cmt)
⇒ ∆BDF = ∆EFD (g-c-g)
⇒ BD = EF (hai cạnh tương ứng)
Do D là trung điểm của AB (gt)
⇒ AD = BD
Mà BD = EF (cmt)
⇒ AD = EF
b) Do AB // EF (gt)
⇒ ∠DAE = ∠FEC (đồng vị)
∠ABC = ∠EFC (đồng vị)
⇒ ∠ADE = ∠EFC
Xét ∆ADE và ∆EFC có:
∠DAE = ∠FEC (cmt)
AD = EF (cmt)
∠ADE = ∠EFC (cmt)
⇒ ∆ADE = ∆EFC (g-c-g)
c) Do ∆ADE = ∆EFC (cmt)
⇒ AE = EC (hai cạnh tương ứng)
DE = FC (hai cạnh tương ứng)
Do ∆BDF = ∆EFD (cmt)
⇒ BF = DE (hai cạnh tương ứng)
Mà DE = FC (cmt)
⇒ BF = FC













 vẽ hình bài6 và làm 2 bài này giúp ạ
vẽ hình bài6 và làm 2 bài này giúp ạ 







