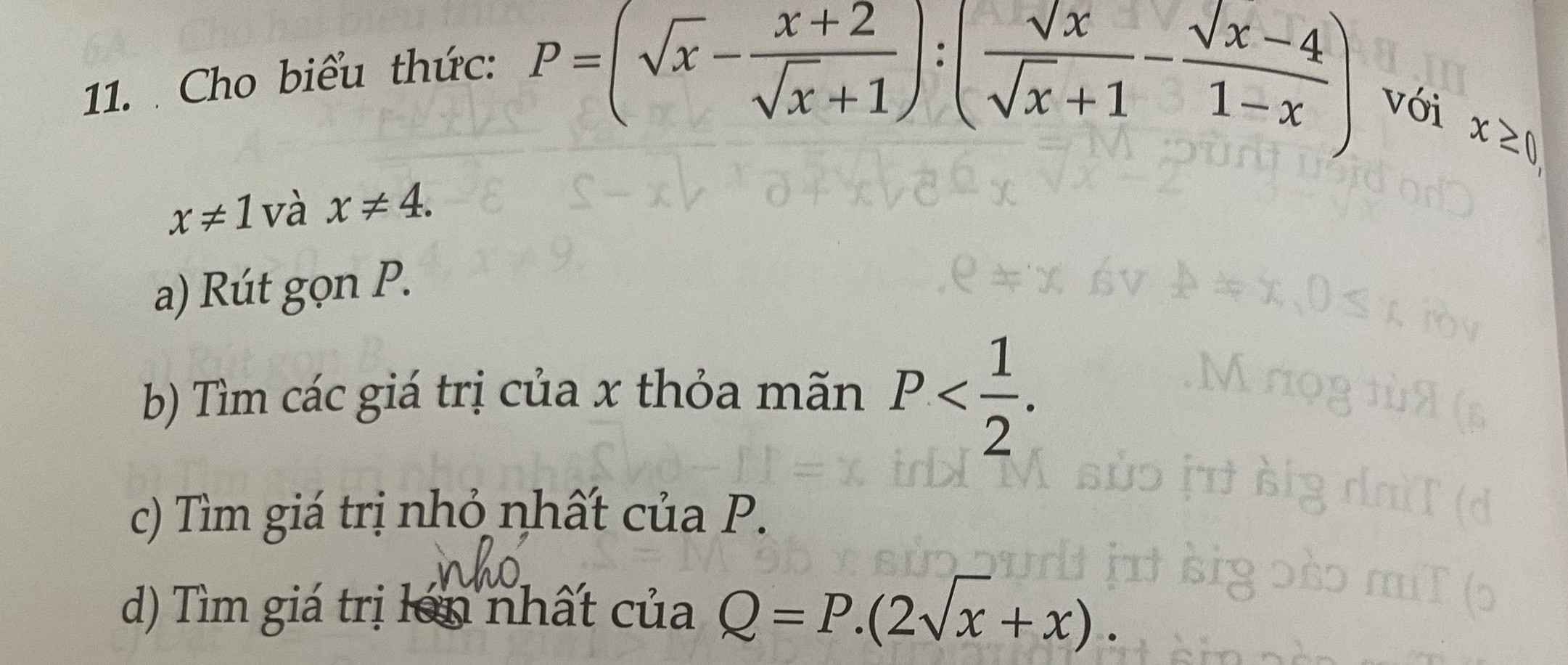a, \(P=\left(\sqrt{x}-\dfrac{x+2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}-4}{1-x}\right)\)
\(=\left(\dfrac{x+\sqrt{x}}{\sqrt{x}+1}-\dfrac{x+2}{\sqrt{x}+1}\right):\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}:\dfrac{x-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}.\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
b, \(P< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}< \dfrac{1}{2}\)
\(\Leftrightarrow2\sqrt{x}-2< \sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}< 4\)
\(\Leftrightarrow0\le x< 16\)
Vậy \(0\le x< 16;x\ne1;x\ne4\).
a: ta có: \(P=\left(\sqrt{x}-\dfrac{x+2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}-4}{x-1}\right)\)
\(=\dfrac{x+\sqrt{x}-x-2}{\left(\sqrt{x}+1\right)}:\dfrac{x-\sqrt{x}+\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-2}{1}\cdot\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
c, \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-3}{\sqrt{x}+2}=1-\dfrac{3}{\sqrt{x}+2}\ge1-\dfrac{3}{2}=-\dfrac{1}{2}\)
\(\Rightarrow minP=-\dfrac{1}{2}\Leftrightarrow x=0\)
b: Để \(P< \dfrac{1}{2}\) thì \(P-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-2-\sqrt{x}-2}{2\left(\sqrt{x}+2\right)}< 0\)
hay x<16
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 16\\x\notin\left\{1;4\right\}\end{matrix}\right.\)
Bạn thử làm xem nếu câu hỏi nào không biết thì mới hỏi nha, chứ đăng như này làm hơi dài á với lại mình thấy bạn hay đăng mấy dạng toán như này, bạn chỉ cần làm tương tự như nhưng bài trước là được :<
a. \(P=\left(\sqrt{x}-\dfrac{x+2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}-4}{1-x}\right)\)
\(=\dfrac{x+\sqrt{x}-x-2}{\sqrt{x}+1}:\dfrac{x-\sqrt{x}+\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}.\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x-4}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{x-4}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
b. Để \(P< \dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{1}{2}< 0\Leftrightarrow\dfrac{\sqrt{x}-4}{2\left(\sqrt{x}+2\right)}< 0\Leftrightarrow\dfrac{\sqrt{x}-4}{2\left(\sqrt{x}+2\right)}>0\)
ta có \(\left\{{}\begin{matrix}\sqrt{x}-4< 0\\2\left(\sqrt{x}+2\right)\ge4>0\end{matrix}\right.\) \(\Rightarrow\sqrt{x}>4\Rightarrow x< 16\)
c. \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}=\dfrac{1-\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=1-\dfrac{3}{\sqrt{x}+2}\)
Ta có với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+2\ge2\Rightarrow\dfrac{3}{\sqrt{x}+2}\le\dfrac{3}{2}\Rightarrow P=1-\dfrac{3}{\sqrt{x}+2}\le-\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(x=0\)
Vậy \(P_{min}=-\dfrac{1}{2}\) khi \(x=0\)
d. Ta có \(Q=P\left(2\sqrt{x}+x\right)=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}+x\right)}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}-1\right)\sqrt{x}\left(2+\sqrt{x}\right)}{\sqrt{x}+2}=\sqrt{x}\left(\sqrt{x}-1\right)=x-\sqrt{x}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall x\)
Dấu "=" xảy ra khi \(x=\dfrac{1}{4}\)
Vậy \(Q_{min}=-\dfrac{1}{4}\) khi \(x=\dfrac{1}{4}\)