a.
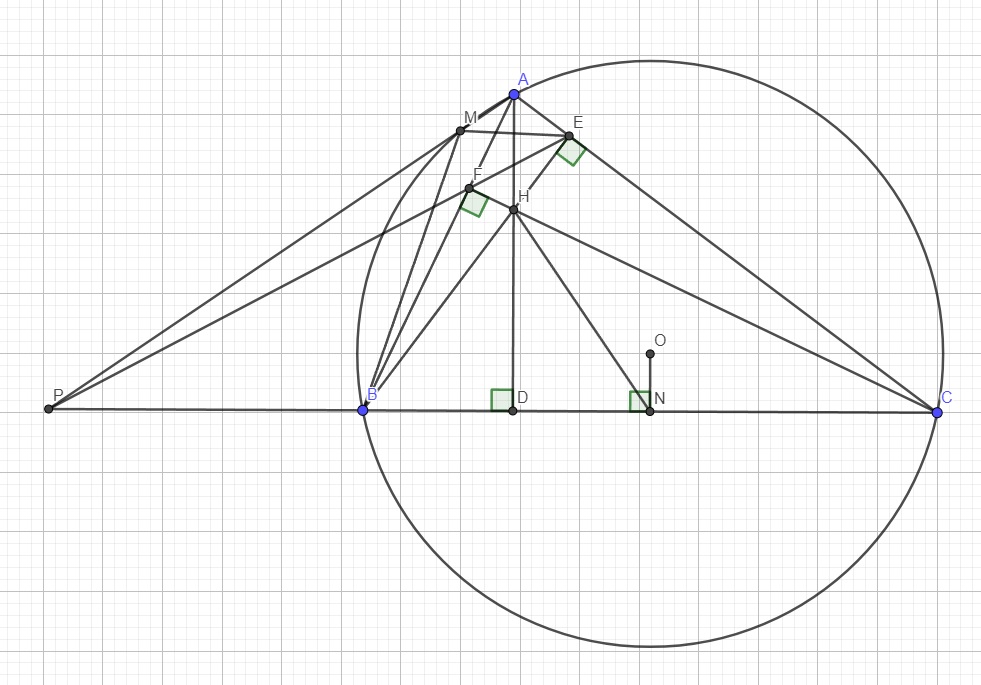
Do H là giao điểm 2 đường cao AD, BE nên H là trực tâm tam giác ABC
\(\Rightarrow CF\) là đường cao thứ 3
\(\Rightarrow CF\perp AB\) tại F
2 điểm E và F cùng nhìn BC dưới 1 góc vuông nên tứ giác BCEF nội tiếp hay 4 điểm B, F, E, C cùng thuộc một đường tròn
b.
Do tứ giác BCEF nội tiếp \(\Rightarrow\widehat{BCE}+\widehat{BFE}=180^0\)
Mà \(\widehat{BFE}+\widehat{BFP}=180^0\)
\(\Rightarrow\widehat{BCE}=\widehat{BFP}\)
Xét hai tam giác PEC và PBF có:
\(\left\{{}\begin{matrix}\widehat{CPE}\text{ chung}\\\widehat{BCE}=\widehat{BFP}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta PEC\sim\Delta PBF\left(g.g\right)\)
\(\Rightarrow\dfrac{PE}{PB}=\dfrac{PC}{PF}\Rightarrow PE.PF=PB.PC\)
Hoàn toàn tương tự, do tứ giác BCAM nội tiếp (O;R) nên \(\widehat{PCA}=\widehat{PMB}\)
\(\Rightarrow\Delta PBM\sim\Delta PAC\left(g.g\right)\)
\(\Rightarrow\dfrac{PB}{PA}=\dfrac{PM}{PC}\Rightarrow PM.PA=PB.PC\)
\(\Rightarrow PM.PA=PE.PF\left(đpcm\right)\)
c.
Do N là trung điểm BC nên N là tâm đường tròn ngoại tiếp BCEF
\(\Rightarrow\widehat{ENF}=2\widehat{ECF}\) (góc ở đỉnh và góc nt cùng chắn BC)
Tứ giác BDHF nội tiếp (D và F cùng nhìn BH dưới 1 góc vuông)
\(\Rightarrow\widehat{ADF}=\widehat{EBF}\) (cùng chắn HF)
Tứ giác BCEF nội tiếp (cm câu a)
\(\Rightarrow\widehat{EBF}=\widehat{ECF}\) (cùng chắn EF)
\(\Rightarrow\widehat{ADF}=\widehat{ECF}\)
Tứ giác CDHE nội tiếp (D và E cùng nhìn CH dưới 1 góc vuông)
\(\Rightarrow\widehat{ECF}=\widehat{EDH}\) (cùng chắn EH)
\(\Rightarrow\widehat{ADF}+\widehat{EDH}=2\widehat{ECF}\)
\(\Rightarrow\widehat{EDF}=2\widehat{ECF}\)
\(\Rightarrow\widehat{EDF}=\widehat{ENF}\)
\(\Rightarrow EFDN\) nội tiếp
\(\Rightarrow\widehat{DNF}=\widehat{DEF}\)
\(\Rightarrow\Delta PNF\sim\Delta PED\left(g.g\right)\)
\(\Rightarrow\dfrac{PN}{PE}=\dfrac{PF}{PD}\Rightarrow PN.PD=PE.PF\)
\(\Rightarrow PN.PD=PM.PA\)
\(\Rightarrow\dfrac{PD}{PM}=\dfrac{PA}{PN}\)
\(\Rightarrow\Delta PDA\sim\Delta PMN\left(c.g.c\right)\) (có góc P chung)
\(\Rightarrow\widehat{PMN}=\widehat{PDA}=90^0\)
Hay \(NM\perp AP\) (1)
Theo câu b ta có \(\dfrac{PE}{PA}=\dfrac{PM}{PF}\Rightarrow\Delta PAF\sim\Delta PEM\left(c.g.c\right)\)
\(\Rightarrow\widehat{MAF}=\widehat{MEF}\Rightarrow AEFM\) nội tiếp
\(\Rightarrow\) 5 điểm A, E, H, F, M cùng thuộc 1 đường tròn
\(\Rightarrow\widehat{AMH}=\widehat{AFH}=90^0\)
\(\Rightarrow HM\perp AP\) (2)
(1);(2) \(\Rightarrow N,H,M\) thẳng hàng
a: Xét ΔABC có
BE,AD là các đường cao
BE cắt AD tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB tại F
Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Ta có: BFEC là tứ giác nội tiếp
=>\(\widehat{FBC}+\widehat{FEC}=180^0\)
mà \(\widehat{FBC}+\widehat{PBF}=180^0\)(hai góc kề bù)
nên \(\widehat{PBF}=\widehat{FEC}=\widehat{PEC}\)
Xét ΔPBF và ΔPEC có
\(\widehat{PBF}=\widehat{PEC}\)
\(\widehat{BPF}\) chung
Do đó: ΔPBF~ΔPEC
=>\(\dfrac{PB}{PE}=\dfrac{PF}{PC}\)
=>\(PB\cdot PC=PF\cdot PE\left(1\right)\)
Ta có: AMBC là tứ giác nội tiếp(A,M,B,C cùng thuộc (O))
=>\(\widehat{AMB}+\widehat{ACB}=180^0\)
mà \(\widehat{AMB}+\widehat{PMB}=180^0\)(hai góc kề bù)
nên \(\widehat{PMB}=\widehat{ACB}=\widehat{PCA}\)
Xét ΔPMB và ΔPCA có
\(\widehat{PMB}=\widehat{PCA}\)
\(\widehat{MPB}\) chung
Do đó: ΔPMB~ΔPCA
=>\(\dfrac{PM}{PC}=\dfrac{PB}{PA}\)
=>\(PM\cdot PA=PB\cdot PC\left(2\right)\)
Từ (1),(2) suy ra \(PE\cdot PF=PM\cdot PA\)








 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn

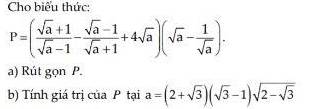



 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn