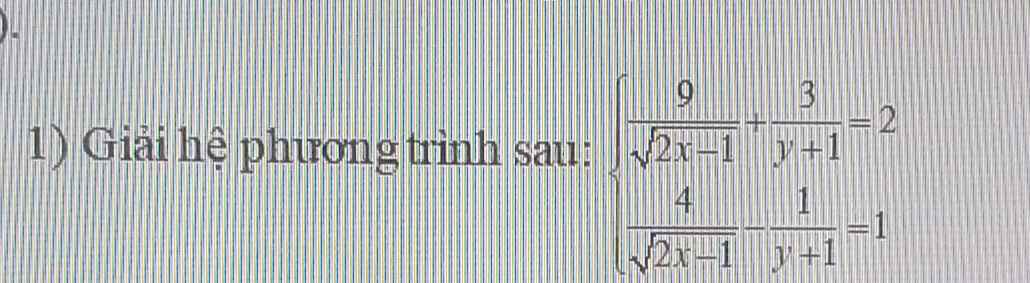\(\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\left(1\right)\\\dfrac{12}{\sqrt{2x-1}}-\dfrac{3}{y+1}=3\left(2\right)\end{matrix}\right.\)
Lấy \(\left(2\right)+\left(1\right)\) ta được:
\(\dfrac{21}{\sqrt{2x-1}}=5\\ \Leftrightarrow5\sqrt{2x-1}=21\\ \Leftrightarrow25\left(2x-1\right)=441\\ \Leftrightarrow50x-25=441\\ \Leftrightarrow50x=466\Leftrightarrow x=\dfrac{233}{25}\)
Thay x vào (1)
\(\dfrac{9}{\sqrt{2\cdot\dfrac{233}{25}-1}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{9}{\sqrt{\dfrac{441}{25}}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{9}{\dfrac{21}{5}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{15}{7}+\dfrac{3}{y+1}=2\\ \Leftrightarrow15\left(y+1\right)+21=14\left(y+1\right)\\ \Leftrightarrow15y+15+21=14y+14\\ \Leftrightarrow y=-22\)
Vậy pt có tập nghiệm \(\left(x;y\right)=\left(\dfrac{233}{25};-22\right)\)
\(\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{36}{\sqrt{2x-1}}+\dfrac{12}{y+1}=8\\\dfrac{36}{\sqrt{2x-1}}-\dfrac{9}{y+1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{21}{y+1}=-1\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+1=-21\\\dfrac{4}{\sqrt{2x-1}}=\dfrac{20}{21}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-22\\2x-1=\dfrac{441}{25}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{233}{25}\\y=-22\end{matrix}\right.\)