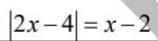\(Ta.có\left|2x-4\right|=2x-4khi2x-4\ge0\Leftrightarrow x\ge2\\ \left|2x-4\right|=-2x+4khi2x-4< 0\Leftrightarrow x< 2\)
Nếu \(x\ge2\) ta có phương trình:
\(2x-4=x-2\\ \Leftrightarrow2x-x=-2+4\\ \Leftrightarrow x=2\left(tm\right)\)
Nếu \(x< 2\) ta có phương trình:
\(-2x+4=x-2\\ \Leftrightarrow-2x-x=-2-4\\ \Leftrightarrow-3x=-6\\ \Leftrightarrow x=2\left(ktm\right)\)
Vậy phương trình có nghiệm là:\(S=\left\{2\right\}\)
\(\left|2x-4\right|=x-2\left(1\right)\)
\(\left|2x-4\right|=\left\{{}\begin{matrix}2x-4\text{ khi }2x-4\ge0\text{ hay }x\ge2\\-\left(2x-4\right)\text{ khi }2x-4< 0\text{ hay }x< 2\end{matrix}\right.\)
\(TH1:2x-4=x-2\)
\(\Leftrightarrow2x-x=4-2\)
\(\Leftrightarrow x=2\left(\text{nhận}\right)\)
\(TH2:-\left(2x-4\right)=x-2\)
\(\Leftrightarrow-2x+4=x-2\)
\(\Leftrightarrow-2x-x=-4-2\)
\(\Leftrightarrow-3x=-6\)
\(\Leftrightarrow x=2\left(\text{loại }\right)\)
\(\text{Vậy phương trình(1)có tập nghiệm là }S=\left\{2\right\}\)
TH1: x>=2
=>2x-4=x-2
=>x=2(nhận)
TH2: x<2
=>4-2x=x-2
=>-3x=-6
=>x=2(loại)