Áp dụng TCDSTLBN, ta có :
\(\dfrac{a}{b+c-a}=\dfrac{b}{c+a-b}=\dfrac{c}{a+b-c}=\dfrac{a+b+c}{b+c-a+c+a-b+a+b-c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b+c-a}=1\\\dfrac{b}{c+a-b}=1\\\dfrac{c}{a+b-c}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=b+c-a\\b=c+a-b\\c=a+b-c\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(S=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\)
\(S=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
Vậy \(S=6\)
Cần xét thêm trường hợp \(a+b+c=0\) nữa
Khi đó \(\left\{{}\begin{matrix}b+c=-a\\c+a=-b\\a+b=-c\end{matrix}\right.\)
Nên \(S=\dfrac{-a}{a}+\dfrac{-b}{b}+\dfrac{-c}{c}=-3\)


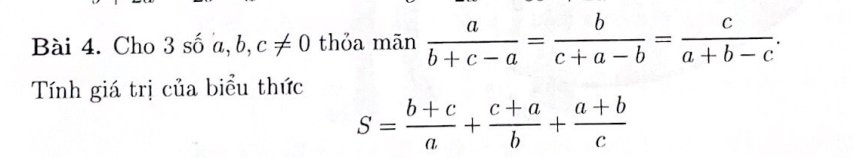 Ét o Ét
Ét o Ét














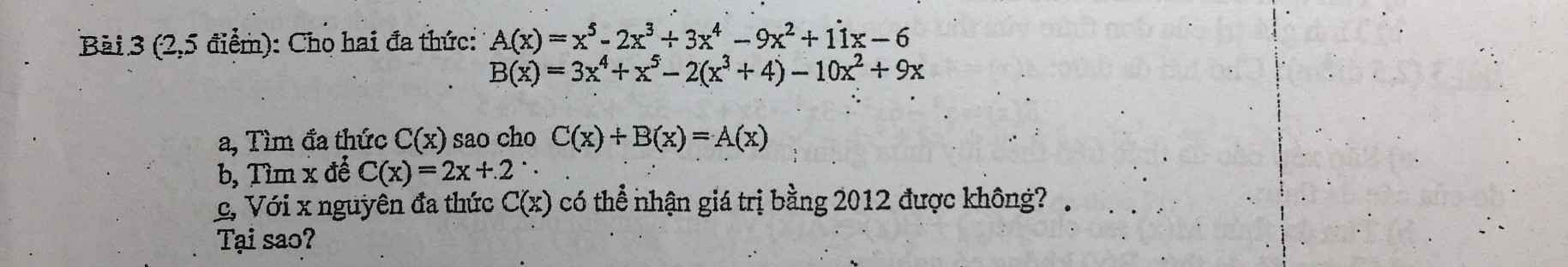 GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT

