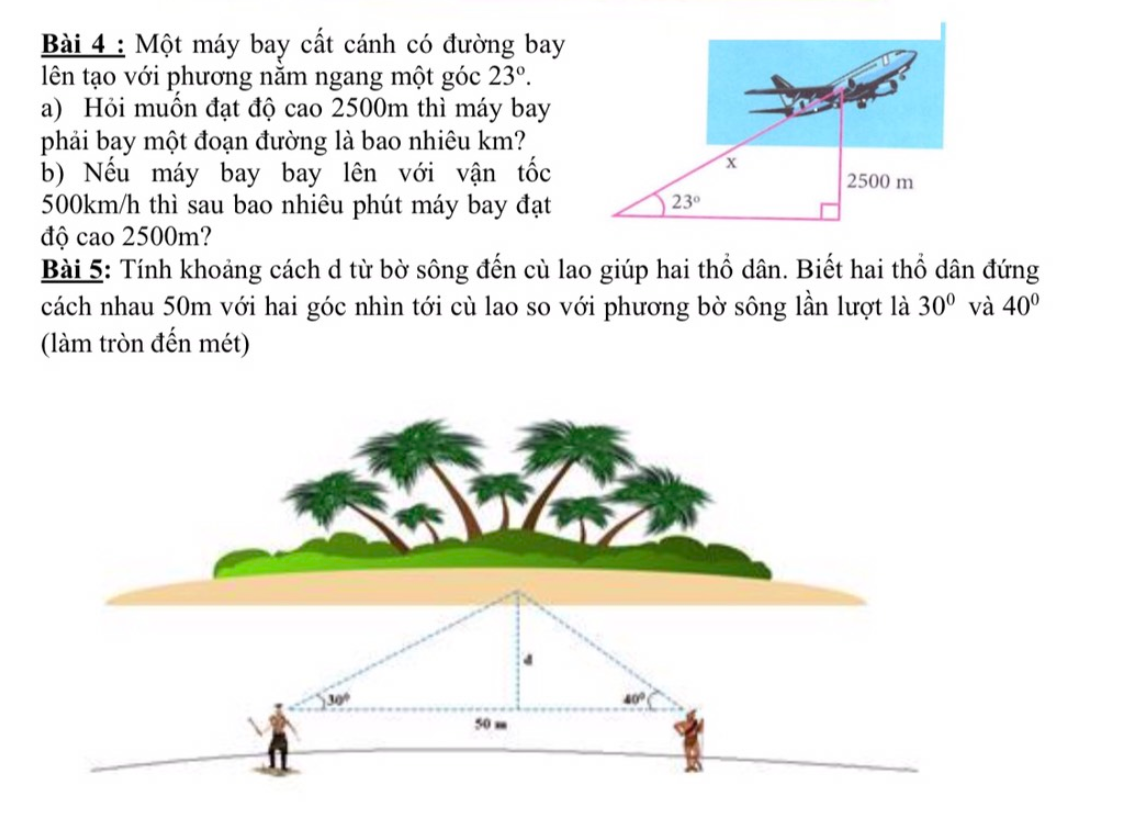
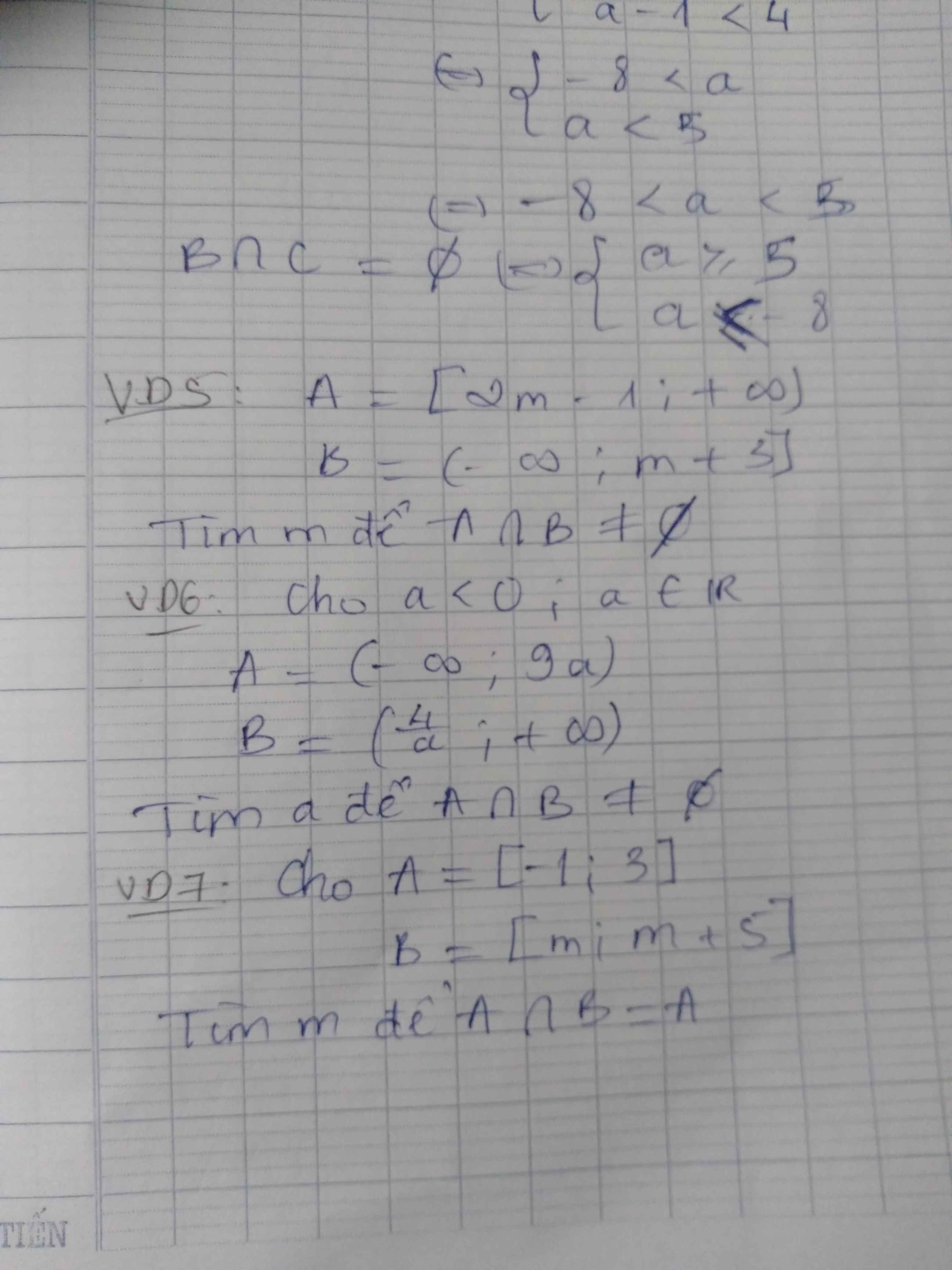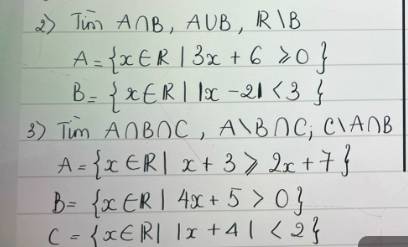cíu vs ạ!
Bài 16. Trong mặt phẳng tọa độ \(Oxy\), cho \(\triangle ABC\) biết \(A(1;2), B(-1;1), C(2;4)\).
a) Chứng minh \(A, B, C\) là ba đỉnh của một tam giác.
b) Tìm tọa độ chân đường cao \(K\) của \(\triangle ABC\).
c) Tính chu vi và diện tích của \(\triangle ABC\).
d) Tìm tọa độ trọng tâm \(G\) của \(\triangle ABC\).
e) Tìm tọa độ tâm \(I\) của đường tròn ngoại tiếp \(\triangle ABC\).
a: \(\overrightarrow{AB}=\left(-1-1;1-2\right)=\left(-2;-1\right)\)
\(\overrightarrow{AC}=\left(2-1;4-2\right)=\left(1;2\right)\)
Vì \(-\frac21<>-\frac12\)
nên A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của một tam giác
c: \(\overrightarrow{BC}=\left(2+1;4-1\right)=\left(3;3\right)\)
\(BC=\sqrt{3^2+3^2}=3\sqrt2\)
\(AB=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{4+1}=\sqrt5\)
\(AC=\sqrt{1^2+2^2}=\sqrt5\)
Chu vi của tam giác ABC là:
\(3\sqrt2+\sqrt5+\sqrt5=3\sqrt2+2\sqrt5\)
Xét ΔABC có \(cosBAC=\frac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\frac{5+5-18}{2\cdot\sqrt5\cdot\sqrt5}=\frac{10-18}{2\cdot5}=\frac{-8}{10}=-\frac45\)
=>\(sinBAC=\sqrt{1-\left(-\frac45\right)^2}=\sqrt{1-\frac{16}{25}}=\sqrt{\frac{9}{25}}=\frac35\)
Diện tích tam giác BAC là:
\(S_{ABC}=\frac12\cdot AB\cdot AC\cdot\sin BAC=\frac12\cdot\sqrt5\cdot\sqrt5\cdot\frac35=\frac32\)
d: Tọa độ trọng tâm G của ΔABC là:\(\begin{cases}x=\frac{1+\left(-1\right)+2}{3}=\frac23\\ y=\frac{2+1+4}{3}=\frac{3+4}{3}=\frac73\end{cases}\)
=>\(G\left(\frac23;\frac73\right)\)
e: Gọi tọa độ của điểm I là I(x;y)
I(x;y); A(1;2); B(-1;1); C(2;4)
\(IA^2=\left(1-x\right)^2+\left(2-y\right)^2=\left(x-1\right)^2+\left(y-2\right)^2\)
\(IB^2=\left(-1-x\right)^2+\left(1-y\right)^2=\left(x+1\right)^2+\left(y-1\right)^2\)
\(IC^2=\left(2-x\right)^2+\left(4-y\right)^2=\left(x-2\right)^2+\left(y-4\right)^2\)
I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC
=>\(\begin{cases}IA^2=IB^2\\ IB^2=IC^2\end{cases}\Rightarrow\begin{cases}\left(x-1\right)^2+\left(y-2\right)^2=\left(x+1\right)^2+\left(y-1\right)^2\\ \left(x+1\right)^2+\left(y-1\right)^2=\left(x-2\right)^2+\left(y-4\right)^2\end{cases}\)
=>\(\begin{cases}x^2-2x+1+y^2-4y+4=x^2+2x+1+y^2-2y+1\\ x^2+2x+1+y^2-2y+1=x^2-4x+4+y^2-8y+16\end{cases}\)
=>-2x-4y+5=2x-2y+2 và 2x-2y+2=-4x-8y+20
=>-4x-2y=-3 và 6x+6y=18
=>4x+2y=3 và x+y=3
=>4x+2y=3 và 2x+2y=6
=>4x-2x=3-6
=>2x=-3
=>x=-1,5
x+y=3
=>y=3-(-1,5)=3+1,5=4,5
Vậy: I(-1,5;4,5)






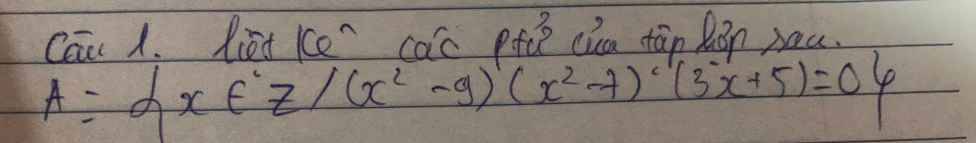 cíu bé vs mn ơi
cíu bé vs mn ơi
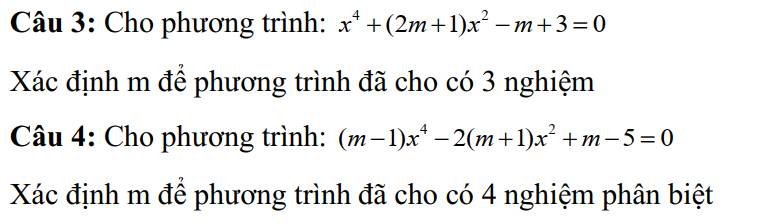 CÍU TUIIII
CÍU TUIIII