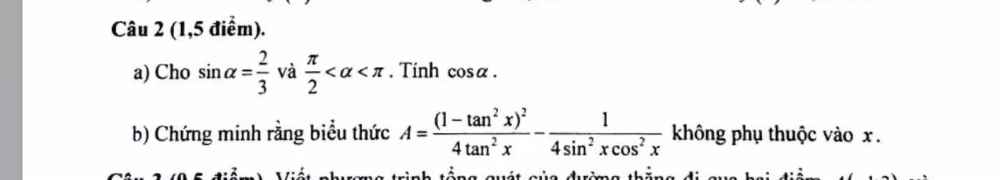\(A=\left\{x\in Z|\left(x^2-9\right)\left(x^2-7\right)\left(3x+5\right)=0\right\}\)
Giải pt \(\left(x^2-9\right)\left(x^2-7\right)\left(3x+5\right)=0\) \(\left(dk:x\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-9=0\\x^2-7=0\\3x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\pm3\left(tm\right)\\x=\pm\sqrt{7}\left(ktm\right)\\x=-\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
Vậy \(A=\left\{-3;3\right\}\)

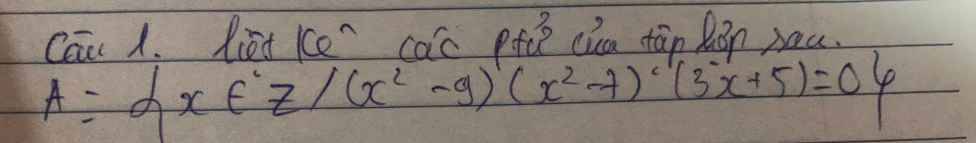 cíu bé vs mn ơi
cíu bé vs mn ơi








 CÍU TUIIII
CÍU TUIIII