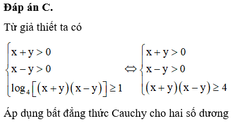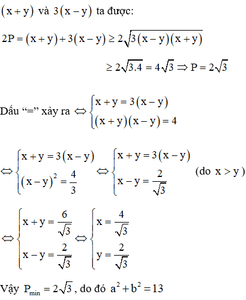Các câu hỏi tương tự
Cho 2 số thực x;y thỏa mãn
x
,
y
≥
1
và
log
3
x
+
1
y
+
1
y
+
1
9...
Đọc tiếp
Cho 2 số thực x;y thỏa mãn x , y ≥ 1 và log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 Biết giá trị nhỏ nhất của biểu thức P = x 3 + y 3 − 57 x + y là một số thực có dạng a + b 7 , a , b ∈ ℤ . Tính giá trị của a+b
A. -28
B. -29
C. -30
D. -31
Cho hai số thực không âm x,y ≤ 1. Biết
P
l
n
(
1
+
x
2
)
(
1
+
y
2
)
+
8
17
(
x
+
y
)
2
có giá trị nhỏ nhất là
-
a
b
+
2
ln
c...
Đọc tiếp
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405
Cho hai số thực dương x, y thỏa mãn
l
o
g
3
(
x
+
y
+
2
)
1
+
l
o
g
3
x
-
1
y
+
y
-
1...
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn l o g 3 ( x + y + 2 ) = 1 + l o g 3 x - 1 y + y - 1 x . Giá trị nhỏ nhất của biểu thức x 2 + y 2 x y = a b với a , b ∈ N và (a,b)=1. Hỏi a+b bằng bao nhiêu
A. 2
B. 9
C. 12
D. 13
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+
y...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3b bằng
A. -2
B. 4
C. -1
D. 5
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3 b bằng
A. -2
B. 4
C. -1
D. 5
Cho hàm số
y
x
+
b
a
x
−
2
có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm
M
1
;
−
2
song song với đường thẳng
3
x
+
y
−
4...
Đọc tiếp
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0
Cho các số thực x,y thay đổi thỏa mãn
log
2
sinx
+
2
cosx
+
2
2
cosx
-
sinx
+
3
. Gọi -
a
b
...
Đọc tiếp
Cho các số thực x,y thay đổi thỏa mãn log 2 sinx + 2 cosx + 2 = 2 cosx - sinx + 3 . Gọi - a b với a ∈ N * , b ∈ N * , a b tối giản là giá trị nhỏ nhất của biểu thức P= 3 cos 3 x + sin 2 x - 5 cosx . Tính T=a+b.
A.T=200.
B. T=257.
C. T=210.
D. T=240
Cho a, b 0 thỏa mãn điều kiện a + b + ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
l
à
x
(
x
-
y
)
4
(
x
,
y
∈
N
)
. Giá trị của x + y là A. 3 B. 5 C. 7 D. 9
Đọc tiếp
Cho a, b > 0 thỏa mãn điều kiện a + b + ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 l à x ( x - y ) 4 ( x , y ∈ N ) . Giá trị của x + y là
A. 3
B. 5
C. 7
D. 9
Cho các số thực không âm x, y thỏa mãn
x
2
+
2
x
-
y
+
1
l
o
g
2
2
y
+
1
x
+
1
. Biết giá trị nhỏ nhất của
P
e
2
x...
Đọc tiếp
Cho các số thực không âm x, y thỏa mãn x 2 + 2 x - y + 1 = l o g 2 2 y + 1 x + 1 . Biết giá trị nhỏ nhất của P = e 2 x - 1 + 4 x 2 - 2 y + 1 = a b ( a , b ∈ Z ) , phần số này tối giản. Giá trị của a 2 + b 2 + 5 là:
A. 17
B. 10
C. 9
D. 39