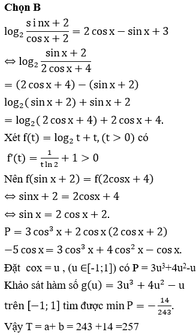Các câu hỏi tương tự
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)-1 và log(sinx+cosx)1/2(logn-1). Giá trị của n là A. 11. B. 12. C. 10. D. 15.
Đọc tiếp
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
sin
x
+
cos
x
-
1
sin
x
-
cos
x
+
3
khi đó: A.
M
-
1
;
...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin x + cos x - 1 sin x - cos x + 3 khi đó:
A. M = - 1 ; m = 1
B. M = 1 7 ; m = - 1
C. M = - 1 7 ; m = 1 7
D. M = - 1 ; m = - 1 7
Tìm giá trị nhỏ nhất của hàm số
y
sin
x
-
cos
x
+
1
sin
x
+
cos
x
+
2
B. 1
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = sin x - cos x + 1 sin x + cos x + 2
![]()
B. 1
![]()
![]()
Cho hàm số
y
sin
x
-
cos
x
+
1
sin
x
+
cos
x
+
2
. Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của
M
+
m
là A. 2 B. 4 C. 0 D....
Đọc tiếp
Cho hàm số y = sin x - cos x + 1 sin x + cos x + 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M + m là
A. 2
B. 4
C. 0
D. 1
Cho hàm số
y
sinx
−
cosx
+
1
sinx
+
cosx
−
2
. Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là A. 1 B. 4 C. 2 D. 0
Đọc tiếp
Cho hàm số y = sinx − cosx + 1 sinx + cosx − 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là
A. 1
B. 4
C. 2
D. 0
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm
2
m
(
c
o
s
x
+
s
i
n
x
)
2
m
2
+
c
o
s
x
-
sin
x
+
3
2
A.
-
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m ( c o s x + s i n x ) = 2 m 2 + c o s x - sin x + 3 2
A. - 1 2 > m < 1 2
B. m = ± 1 2
C. - 1 4 > m < 1 4
D. m = ± 1 4
Cho
x
∈
0
;
π
2
. Biết
log
sin
x
+
logcos
x
-
1
và
log
sin
x
+
cos
x
1
2
log
n...
Đọc tiếp
Cho x ∈ 0 ; π 2 . Biết log sin x + logcos x = - 1 và log sin x + cos x = 1 2 log n - 1 . Giá trị của n là
A. 11
B. 12
C. 10
D. 15
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số
y
sin
x
+
2
cos
x
+
1
s
i
n
x
+
cos
x
+
2
là A.
m...
Đọc tiếp
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 s i n x + cos x + 2 là
A. m = − 1 2 ; M = 1.
B. m = 1 ; M = 2.
C. m = − 2 ; M = 1.
D. m = − 1 ; M = 2.
Cho hai số thực dương x, y thỏa mãn
l
o
g
3
(
x
+
y
+
2
)
1
+
l
o
g
3
x
-
1
y
+
y
-
1...
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn l o g 3 ( x + y + 2 ) = 1 + l o g 3 x - 1 y + y - 1 x . Giá trị nhỏ nhất của biểu thức x 2 + y 2 x y = a b với a , b ∈ N và (a,b)=1. Hỏi a+b bằng bao nhiêu
A. 2
B. 9
C. 12
D. 13