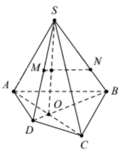
a) + Trong mp(ABCD), AB cắt CD tại E.
E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ Trong mp(SCD), EM cắt SD tại P.
Ta có:
P ∈ SD
P ∈ EM ⊂ mp(MAB)
Vậy P = SD ∩ mp(MAB)
Gọi O là giao điểm AC và BD
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (SBD), nối BN cắt SO tại P
\(\Rightarrow P\in SO\in\left(SAC\right)\)
\(\Rightarrow P=BN\cap\left(SAC\right)\)