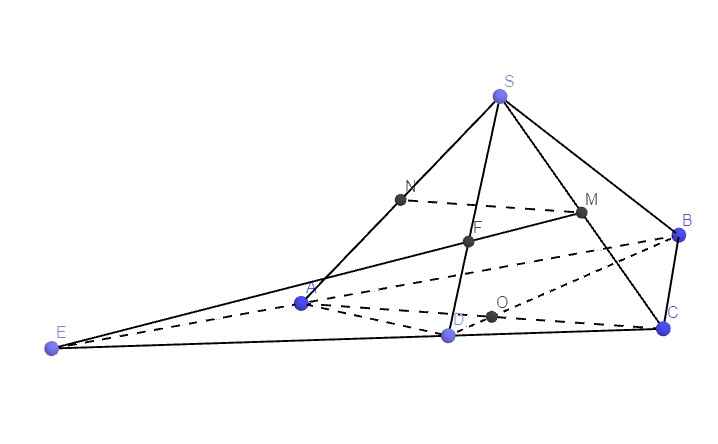
a.
Do M là trung điểm SC, N là trung điểm SA \(\Rightarrow MN\) là đường trung bình tam giác SAC
\(\Rightarrow MN||AC\)
Mà \(AC\in\left(ABCD\right)\Rightarrow MN||\left(ABCD\right)\)
Gọi O là giao điểm AC và BD \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
Trong mp (ABCD), kéo dài AB và CD cắt nhau tại E
Trong mp (SCD), nối EM cắt SD tại F
\(\Rightarrow F=SD\cap\left(MAB\right)\)