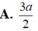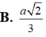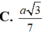Question

cho tứ điện ABCD có các cạnh bằng nhau và bằng 10.gọi E là điểm thuộc cạnh AB sao cho AE=2EB,F là điểm thuộc cạnh BC sao cho BF=2FC và G là điểm thuộc cạnh CD sao cho CG=2GD.độ dài đoạn giao tuyến của (EFG) và mặt bên (ACD) bằng bao nhiêu

Answer 1

\(AE=2EB\Rightarrow\dfrac{AE}{EB}=2\)

\(BF=2FC\Rightarrow\dfrac{BF}{FC}=2\)

\(CG=2DG\Rightarrow\dfrac{DG}{GC}=\dfrac{1}{2}\)

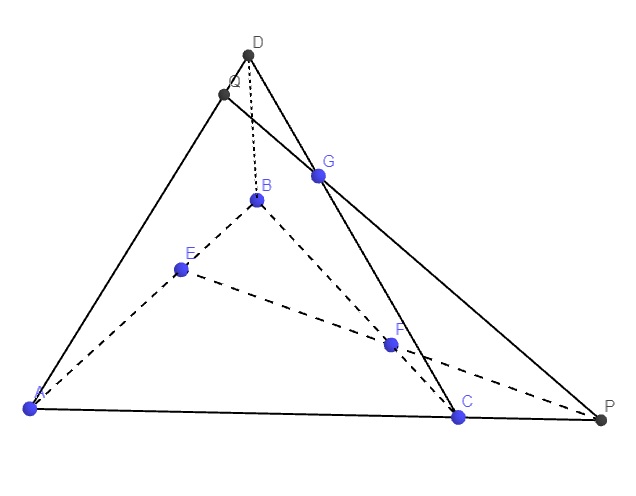
Trong mp (ABC), nối EF kéo dài cắt AC tại P

Trong mp (ACD), nối PG kéo dài cắt AD tại Q

\(\Rightarrow QG=\left(EFG\right)\cap\left(ACD\right)\)

Áp dụng định lý Menelaus cho tam giác ABC:

\(\dfrac{AE}{EB}.\dfrac{BF}{FC}.\dfrac{CP}{PA}=1\Leftrightarrow2.2.\dfrac{CP}{PA}=1\)

\(\Rightarrow\dfrac{CP}{PA}=\dfrac{1}{4}\)

Áp dụng định lý Menelaus cho tam giác ACD:

\(\dfrac{CP}{PA}.\dfrac{AQ}{QD}.\dfrac{DG}{GC}=1\Leftrightarrow\dfrac{1}{4}.\dfrac{AQ}{QD}.\dfrac{1}{2}=1\)

\(\Rightarrow8QD=AQ=AD-QD\)

\(\Rightarrow QD=\dfrac{1}{9}AD=\dfrac{10}{9}\)

\(CG=2GD\Rightarrow DG=\dfrac{1}{3}DC=\dfrac{10}{3}\)

\(AD=CD=AC=10\Rightarrow\Delta ACD\) đều

\(\Rightarrow\widehat{QDG}=60^0\)

Áp dụng định lý hàm cos cho tam giác DQG:

\(QG=\sqrt{DQ^2+DG^2-2DQ.DG.cos\widehat{QDG}}=\dfrac{10\sqrt{7}}{9}\)

Answer 2