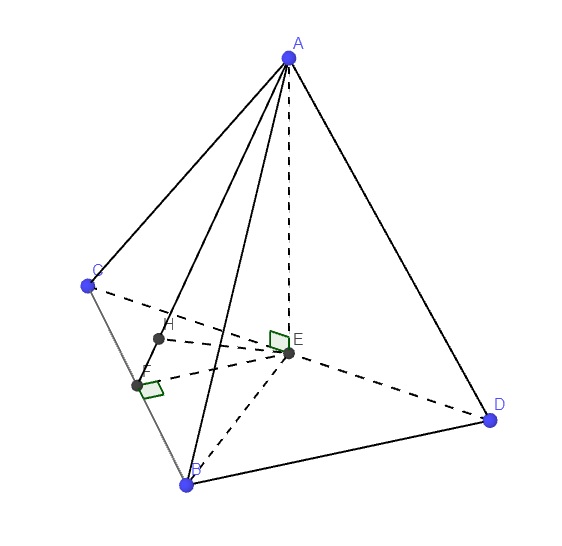
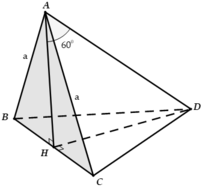
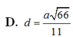Gọi E là trung điểm CD \(\Rightarrow AE\perp CD\Rightarrow AE\perp\left(BCD\right)\)
Hình chóp trên có 1 mp đối xứng là mp (ABE)
b.
Kẻ \(EF\perp BC\left(F\in BC\right)\)
\(\Rightarrow BC\perp\left(AEF\right)\)
\(\Rightarrow\widehat{AFE}\) là góc giữa (ABC) và (BCD)
\(\Delta BCE\) vuông cân tại E \(\Rightarrow EF=\dfrac{BC}{2}=\dfrac{a}{2}\)
\(AE=\dfrac{CD\sqrt{3}}{2}=\dfrac{BC\sqrt{6}}{2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow tan\widehat{AFE}=\dfrac{AE}{EF}=\sqrt{6}\) \(\Rightarrow\widehat{AFE}\approx67^047'\)
c.
Do (ABE) là mặt đối xứng của chóp, \(\Rightarrow d\left(C;\left(ABD\right)\right)=d\left(D;\left(ABC\right)\right)\)
Mà \(DC=2EC\Rightarrow d\left(D;\left(ABC\right)\right)=2d\left(E;\left(ABC\right)\right)\)
Từ E kẻ \(EH\perp AF\Rightarrow EH\perp\left(ABC\right)\Rightarrow EH=d\left(E;\left(ABC\right)\right)\)
Hệ thức lượng: \(EH=\dfrac{AE.EF}{\sqrt{AE^2+EF^2}}=\dfrac{a\sqrt{42}}{14}\)
\(\Rightarrow d\left(C;\left(ABD\right)\right)=2EH=\dfrac{a\sqrt{42}}{7}\)