Đáp án A
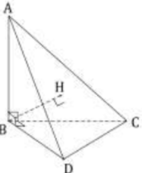

Công thức giải nhanh: Nếu hình chóp O.ABC có OA, OB và OC đôi một vuông góc với nhau thì
![]()
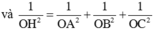
Đáp án A


Công thức giải nhanh: Nếu hình chóp O.ABC có OA, OB và OC đôi một vuông góc với nhau thì
![]()
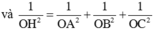
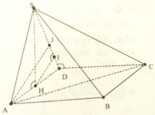
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=BC=a 3 , S A B ^ = S C D ^ = 90 0 và khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC theo a.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a 2 , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4 a 3 /3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
A. h = 2 3 a
B. h = 4 3 a
C. h = 8 3 a
D. h = 3 4 a
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a . Khoảng cách từ A đến mặt phẳng (SBC) bằng
A. 2 5 a 5
B. 5 a 3
C. 2 2 a 3
D. 5 a 5
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c. Tính khoảng cách từ E đến mặt phẳng (SAB).
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC=a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2a 6 . Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2 a 2 , AB = a 2 ; BC = 2a. Gọi M là trung điểm của DC. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
A. 4 a 10 15
B. 3 a 10 5
C. 2 a 10 5
D. 3 a 10 15
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D, A B C ^ = 30 0 . Biết A C = a , C D = a 2 , S A = a 3 2 và cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:
![]()
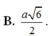
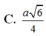
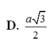
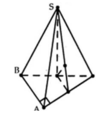
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , A B = 1 , A C = 3 . Tam giác SBC đều và nằm trong mặt phắng vuông với đáy. Tính khoảng cách từ B đến mặt phẳng (SAC)
A. 39 13
B. 1
C. 2 39 13
D. 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao S O = a 3 và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a
A. a 3 3 .
B. 2 a 3 .
C. a 3 2 .
D. a