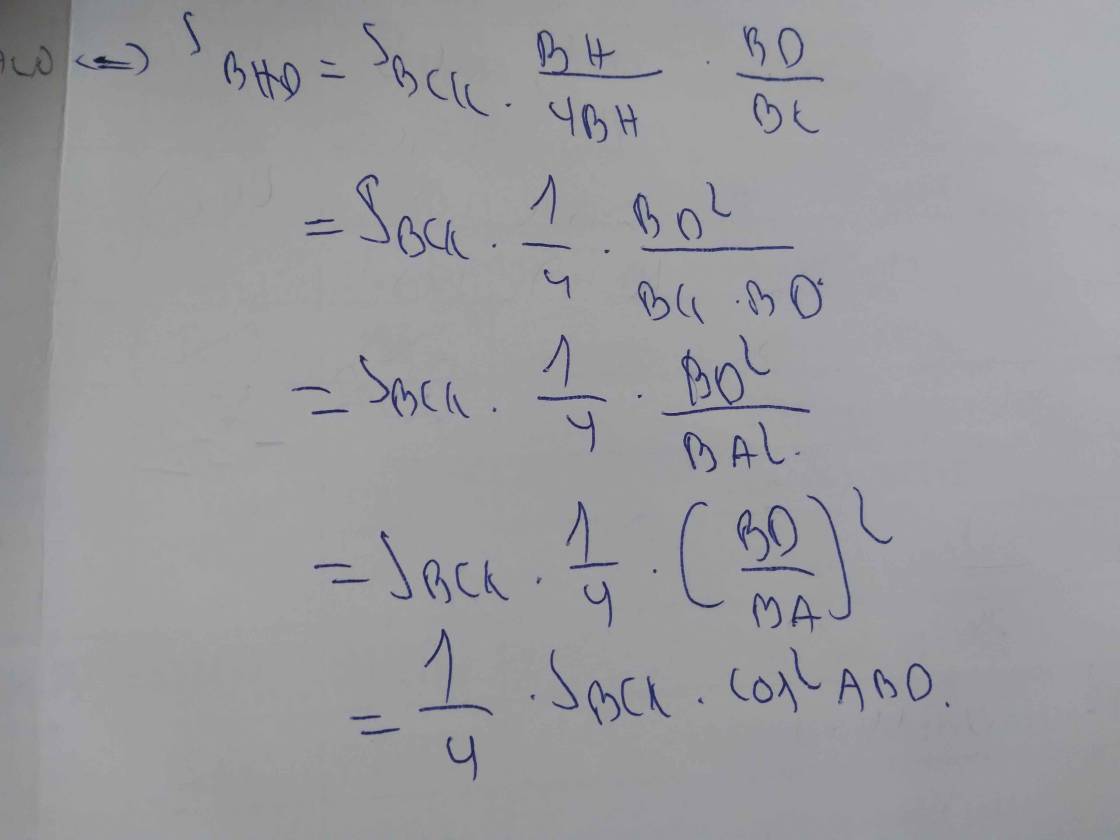Các câu hỏi tương tự
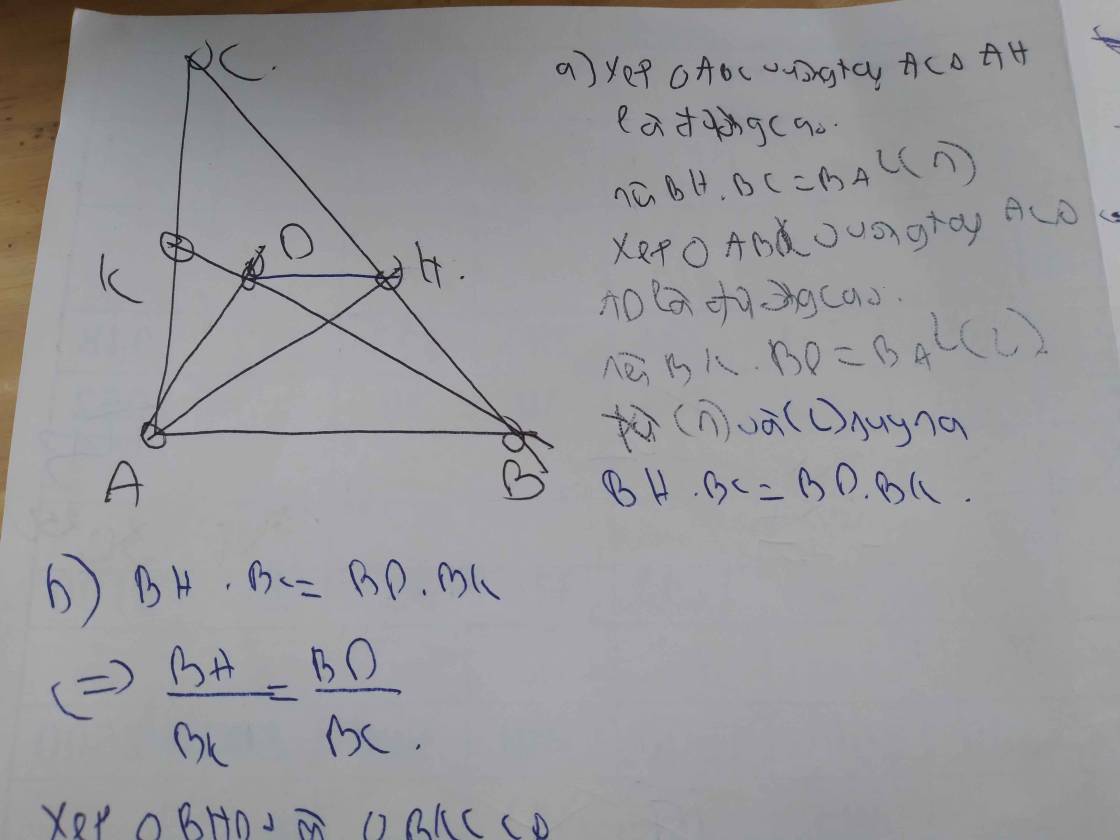
Cho tam giác ABC vuông tại A,đường cao AH .Biết BC=8cm,BH=2cm a) Tính AB,AC,AH b) Trên cạnh AC lấy điểm K (K khác A,C),gọi D là hình chiếu của A trên BK. Chứng minh rằng :BD.BK=BH.BC c) Chứng minh rằng : diện tích BHD =1/4 diện tích BKC×CoS bình phương góc ABD
Bài 4 (3,5 điểm).
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
Tính độ dài các đoạn thẳng AB, AC, AH.
Trên cạnh AC lấy điểm K tùy ý (K thuộc A, K thuộc C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
Cho tam giác ABC vuông tại A, đường cao AH. Trên AC lấy điểm K ( K≠A, K≠C), gọi D là hình chiếu của A trên BK. Cho biết BC = 4BH chứng minh rằng:
SBHD = \(\frac{1}{4}\)SBKC.cos2ABD
mọi người giúp mk vs nha mk cần gấp
Cho tam giác ABC vuông tại A, đường cao AH. Trên AC lấy điểm K ( K≠A, K≠C), gọi D là hình chiếu của A trên BK. Cho biết BC = 4BH chứng minh rằng:
SBHD = \(\frac{1}{4}\)SBKC.cos2ABD
mọi người giúp mk vs nha mk cần gấp
Cho tam giác ABC vuông tại A, đường cao AH, biết BC=8cm, AB=4cm.
a) Giải tam giác vuông ABC
b) Tính AH,BH,HC
c) Trên cạnh AC lấy điểm K (K khác A, K khác C). Gọi D là hình chiếu của A trên BK. Chứng minh BD.BK=BH.BC
Cho tam giác ABC vuông tại A, kể đường cao AH. Biết BH = 2 cm, BC = 8 cm.
a)Tính AB. AC và AH
b)Tính BAB
c)Trên cạnh AC lấy điểm K tùy ý (K khác A và C),gọi D là hình chiếu của A lên BK. Chứng minh AB=BC.sin BDH
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC= 8cm, BH = 2cm
a)Tính độ dài AB,AC,AH
b)Trên cạnh AC lấy điểm K ( K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK.C/m rằng BD.BK = BH.BC
c)C/m rằng SBHD = \(\dfrac{1}{4}\)SBKC cos2 góc ABD
Cho ABC vuông tại A, đường cao AH a) Cho biết BH = 2cm, HC = 4cm. Tính AH, AB và b) Kẻ phân giác của cắt BC tại D. Lấy điểm E trên AC sao cho DE // AH. Gọi K là giao điểm của AD và BE. Chứng minh rằng: BE . BK = BH . BC
Cho tam giác ABC vuông tại A, ABAC, đường cao AH.a) Giả sử BH 4 cm, CH 5 cm. Tính độ dài AB và số đo góc B (làm tròn đến độ) b) Trên cạnh AC lấy điểm D (D khác A và C). Gọi K là hình chiếu của A trên BD.Chứng minh: BK.BDBH.BC và tam giác BKH đồng dạng với tam giác BCD. c) Chứng minh: 4 điểm A, B, K, H cùng thuộc một đường tròn. Xác định tâm O của đường tròn đó.d) Gọi M và N lần lượt là hình chiếu của A và B trên HK. E là giao điểm thức hai của đường thẳng AM với (O). Chứng minh BE // MN.help m...
Đọc tiếp
Cho tam giác ABC vuông tại A, AB<AC, đường cao AH.
a) Giả sử BH = 4 cm, CH = 5 cm. Tính độ dài AB và số đo góc B (làm tròn đến độ) b) Trên cạnh AC lấy điểm D (D khác A và C). Gọi K là hình chiếu của A trên BD.
Chứng minh: BK.BD=BH.BC và tam giác BKH đồng dạng với tam giác BCD. c) Chứng minh: 4 điểm A, B, K, H cùng thuộc một đường tròn. Xác định tâm O của đường tròn đó.
d) Gọi M và N lần lượt là hình chiếu của A và B trên HK. E là giao điểm thức hai của đường thẳng AM với (O). Chứng minh BE // MN.
help mik câu C D với :(