Question

cho tam giác ABC vuông tại A có AB=3cm ac=4cm

a) tính BC.so sánh các góc của tam giác ABC

b) Từ A kẻ đường vuông góc với BC của tam giac ABC.Trên tia BH lấy điểm D sao cho H là trung điểm của đoạn thẳng BD.Chứng minh tam giác ABD cân tại A

c) trên tia AH lấy M sao cho H là trung điểm của AM.Chứng minh tam giác ABM cân 

Giúp mik với cần gấp

Answer 1

Ap dụng định lý py ta go ta có 
\(BC^2=AB^2+AC^2\\ BC^2=9+16=25\\ BC=5\left(cm\right)\)
 

Answer 2

xét tg ABH và tg ADH 
g AHB = g AHD (=90^o) 
AH chung 
BH = DH (gt) 
=> 2 tg = nhau (c-g-c) 
=> AB = AD (2 cạnh t/ư) 
=> tg ABD cân tại A(đpcm) 

Answer 3

Answer 4

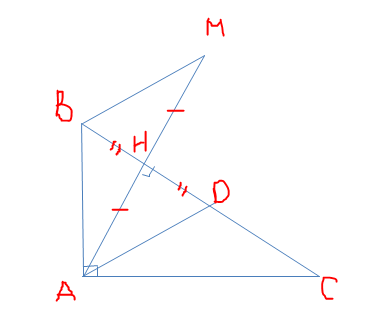
a/Xét \(\Delta ABC\) vuông tại A

=>\(BC^2=AB^2+AC^2\)

=> \(BC^2=9+16=25\)

=>\(BC^2=5^2=>BC=5\left(cm\right)\)

Ta có: \(BC\)\(>\)  \(AC>AB\)

=> \(\widehat{A}>\widehat{B}>\widehat{C}\) ( t/c: cạnh và góc đối diện)

b/ Xét \(\Delta\)vuông \(ABH\) và \(\Delta\) vuông \(ADH\) có:

AH chung

HB = HD ( gt)
=>\(\Delta AHB=\Delta AHD\left(2cgv\right)\)

=> AB = AD ( 2 cạnh tương ứng)

=> \(\Delta ABD\) cân ( cân tại A)

c/ Xét \(\Delta\) vuông \(AHB\) và \(\Delta\) vuông \(MHB\).Có:

BH chung

AH = MH ( gt)

=>\(\text{​​}\Delta AHB=\Delta MHB\left(2cgv\right)\)

=> AB = MB

=> \(\Delta ABM\) cân ( cân tại B)

~ Chúc cậu học tốt~

Answer 5

vì góc BHA = 90^o nên g BHM = 180^o - 90^o = 90^o => gBHM = g BHA = 90^o
xét tg BAH và tg BMH có 
gBHM = g BHA ( cmt) 
AH=HM (GT) 
BH : CHUNG 
=> 2 tg bằng nhau (c-g-c) 
=> AB = BM (2 cạnh t.ư ) 
=> tg ABM cân