Question

cho tam giác ABC trên tia đối của tia AB lấy điểm E, trên tia đối của tia AC lấy điểm D. Gọi M la giao điểm của 2 tia p/g của các góc ACB và AED. Gọi N là giao điểm của ME và AD. Gọi S thứ tự là giao điểm của MC và AB. CMR Góc EMC = (ABC+ADE):2

Answer 1

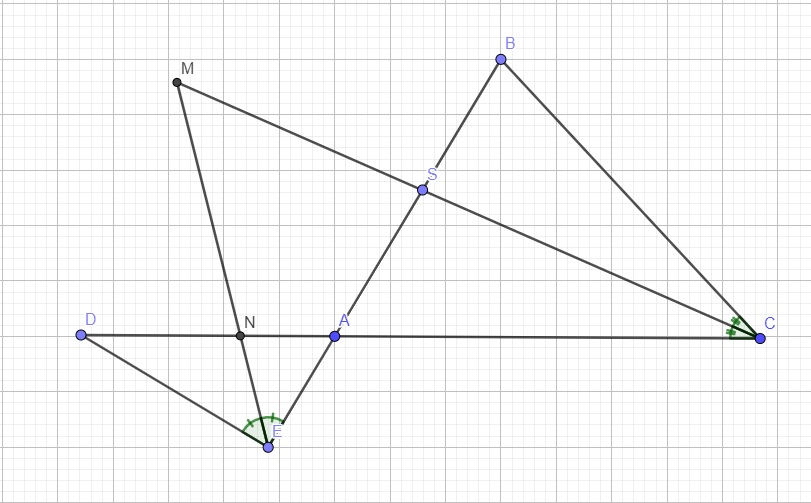
Theo tính chất góc ngoài của tam giác, ta có: \(\widehat{MND}=\widehat{MED}+\widehat{D}\)

\(\widehat{MND}=\widehat{MCD}+\widehat{M}\)

\(\Rightarrow\widehat{MED}+\widehat{D}=\widehat{MCD}+\widehat{M}\) (1)

Tương tự: \(\widehat{BSC}=\widehat{BEM}+\widehat{M}=\widehat{BCM}+\widehat{B}\) (2)

Cộng vế (1) và (2):

\(2\widehat{M}+\widehat{MCD}+\widehat{BEM}=\widehat{B}+\widehat{D}+\widehat{MED}+\widehat{BCM}\)

Mà \(\left\{{}\begin{matrix}\widehat{MCD}=\widehat{BCM}\\\widehat{BEM}=\widehat{MED}\end{matrix}\right.\) theo giả thiết

\(\Rightarrow2\widehat{M}=\widehat{B}+\widehat{D}\Rightarrow\widehat{M}=\dfrac{\widehat{B}+\widehat{D}}{2}\)

Answer 2