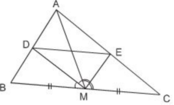
áp dụng t/c đường phân giác vào tam giác AMB có :
\(\dfrac{ME}{AB}=\dfrac{AM}{MB}\left(1\right)\)
áp dụng t/c đường phân giác vào tam giác AMC có :
\(\dfrac{MF}{AC}=\dfrac{AM}{MC}\left(2\right)\)
mà AB = AC ; MB=MC
từ (1) và (2) suy ra : ME= MF (đpcm)
Ta có
\(\widehat{AME}=\widehat{EMB}\left(vì.ME.là.p/giác.\widehat{AMB}\right)\)
\(\widehat{AMF}=\widehat{FMC}\left(vì.MF.là.p/giác\widehat{AMC}\right)\)
\(\Rightarrow\widehat{EMB}=\widehat{FMC}\)
Xét \(\Delta EMB.và.\Delta FMC\)
MB = MC ( vì AM là trung tuyến )
\(\widehat{B}=\widehat{C}\)
\(\widehat{EMB}=\widehat{FMC}\left(cmt\right)\)
Vậy .........
=> ME = MF(2 cạnh tương ứng)