Chọn đáp án B
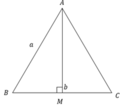
A B = a , B C = b ⇒ A M = a 2 - b 2 4
độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân
![]()
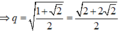
Chọn đáp án B

A B = a , B C = b ⇒ A M = a 2 - b 2 4
độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân
![]()
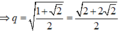
Cho tam giác ABC cân tại A, có đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.
A. 2 2 + 1
B. 1 2 2 + 1
C. 1 2 2 2 + 1
D. 2 + 1
Cho tam giác ABC cân tại A, đường cao AH. Các cạnh BC, AH, AB theo thứ tự lập thành một cấp số nhân. Tính công bội q của dãy số đó
A. 1 2 2 ( 2 + 1 )
B. 2 + 1
C. 2 ( 2 + 1 )
D. 1 2 2 + 1
Ba số x, y, z theo thứ tự lập thành một cấp số nhân có công bội q ≠ 1 . Đồng thời , các số x , 2 y , 3 z theo thứ tự đó lập thành một cấp số cộng có công sai khác 0. Khi đó công bội q bằng
A. - 1 3
B. 3
C. 1 3
D. -3
Cho cấp số nhân ( u n ) có công bội q và u 1 > 0 . Điểu kiện của q để cấp số nhân ( u n ) có ba số hạng liên tiếp là độ dài ba cạnh của một tam giác là
A. 0 < q ≤ 1
B. 1 < q < 1 + 5 2
C. q ≥ 1
D. - 1 + 5 2 < q < 1 + 5 2
Số hạng thứ hai, số hạng đầu và số hạng thứ ba của một cấp số cộng với công sai khác 0 theo thứ tự đó lập thành một cấp số nhân với công bội q. Tìm q ?
A. q= 2
B. q = -2
C. q = − 3 2 .
D. q = 3 2 .
1) cho cấp số nhân \(\left(u_n\right)\) có \(u_2=2\), \(u_6=32\) công bội của cấp số nhân đó là
2) cho cấp số nhân \(\left(u_n\right)\) có số hạng đầu \(u_1=2\) và công bội q = 3. Gía trị \(u_{2019}\) bằng
Cho cấp số nhân ( u n ) có số hạng đầu u 1 = 6 và công bội q = 2. Số hạng thứ tư của cấp số nhân đó bằng
A. 24
B. 96
C. 12
D. 48
Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 ; đồng thời các số x ; 2y ; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q.
A. q = 1 3 .
B. q = 1 9 .
B. q = − 1 3 .
D. q = − 3.
Cho cấp số nhân (un), với u1=1 và công bội q=\(\dfrac{1}{2}\).
a) So sánh |q| với 1.
b) Tính Sn=u1+u2+...+un.. Từ đó, hãy tính limSn.