Chọn đáp án A
Giả sử số phức z = x + y i , x , y ∈ R có điểm biểu diễn là M(x;y)
Ta có 1 + z 2 = x + 1 2 - y 2 + 2 y x + 1 i là số thực nên
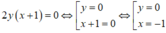
Vậy tập hợp các điểm M(x,y) biểu diễn số phức z = x +yi là hai đường thẳng y = 0; x = -1.
Chọn đáp án A
Giả sử số phức z = x + y i , x , y ∈ R có điểm biểu diễn là M(x;y)
Ta có 1 + z 2 = x + 1 2 - y 2 + 2 y x + 1 i là số thực nên
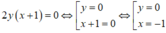
Vậy tập hợp các điểm M(x,y) biểu diễn số phức z = x +yi là hai đường thẳng y = 0; x = -1.
Cho các số phức z thỏa mãn z + 1 - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức z là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3=0
B. 4x+6y+3=0
C. 4x-6y+3=0
D. 4x-6y-3=0
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Xét các số phức z thỏa mãn z - 1 = 1 + i z . Biết rằng tập hợp tất cả các điểm biểu diễn số phức w = 1 + 2 i z + 2 là một đường tròn, đường tròn đó tiếp xúc với đường thẳng nào dưới đây?
A. d 1 : 3 x + y - 1 = 0
B. d 1 : x - 3 y - 3 = 0
C. d 1 : 3 x - y - 1 = 0
D. d 1 : x + 3 y + 3 = 0
Cho các số phức z thỏa mãn |z+1-i|=|z-1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3= 0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.
Tập hợp các điểm biểu diễn số phức z thỏa mãn là đường thẳng z - 1 + i = z + 1 - 2 i là đường thẳng ∆ : a x + b y + c = 0 . Tính ab + c
A. 15
B. 9
C. 11
D. 6
Cho số phức z thỏa mãn z + i = 1 . Biết rằng tập hợp các điểm biểu diễn các số phức w = z − 2 i là một đường tròn. Tâm của đường tròn đó là:
A. I(0;-1)
B. I(0;-3)
C. I(0;3)
D. I(0;1)
Cho số phức z thỏa mãn | z - 2 i | = m 2 + 4 m + 6 với m là số thực. Biết rằng tập hợp các điểm biểu diễn của số phức w = (4-3i)z+2i là đường tròn. Bán kính của đường tròn đó có giá trị nhỏ nhất bằng
A. 10
B. 2
C. 10
D. 2
Cho số phức z thỏa mãn z + 3 - i z ¯ + 1 + 3 i là một số thực. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng:
B. 0.
B. 0.
C. 2 2
D. 3 2
Cho số phức z thỏa mãn z - 2 = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = ( 1 - i ) z + i là một đường tròn. Tính bán kính r của đường tròn đó
A. 2 2
B. 4
C. 2
D. 2