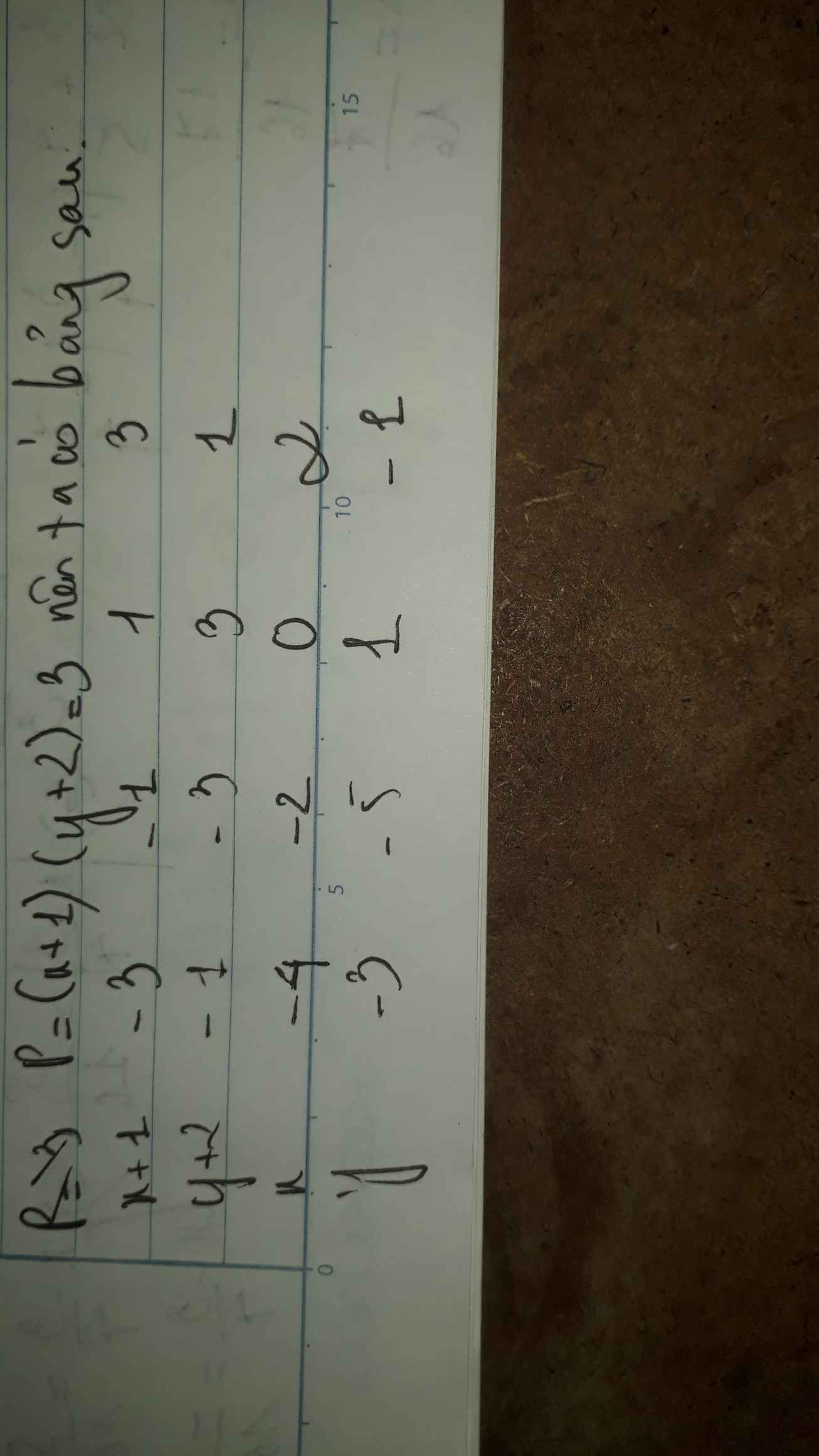Bài 11: Chia đa thức cho đơn thức
Các câu hỏi tương tự
tìm các giá trị nguyên x sao cho A chia hết cho B:
a/ A=3x3+4x2-7x+5 và B=x-3
b/A=x4+4x3-2x+15 và B=x+6
c/A=3x3-2x2+5x-2 và B=x2+1
Giúp mình giải bài này trong tuần này với!
tìm x nguyên thỏa mãn:
x^3 - 8x^2 + 2x chia hết cho x^2 +1
Xem chi tiết
Câu 1: Phép chia đa thức ( x – y )2 cho đa thức ( y – x )2
Câu 2 : Rút gọn biểu thức P =(x + y)2 + (x - y)2 + 2(x + y)(x- y)
Câu 3 : Giá trị của biểu thức x2 + 2x + 1 tại x = -1
Câu 4 : Một hình chữ nhật có hai cạnh kề bằng 4cm và 6cm. Tính độ dài đường chéo của hình chữ nhật đó
tìm x,y,z sao cho:
x2+y2+2z2+4x-4y-6z-2xz+9=0
Bài 1: chia đa thức cho đa thức:
a, ( x3 + 8y3) : (2y+ x)
b, ( x3 + 3x2y+ 3xy2 + y3): (2x+2y)
c, ( 6x5y2 - 9x4y3 + 15x3y4) : 3x3y2
d, (2x3- 21x2 + 67x - 60) : (x-5)
e, ( x4 + 2x3 +x - 25) : (x2 +5)
f, (27x3 -8) : ( 6x + 9x2 +4)
Đọc tiếp
Bài 1: chia đa thức cho đa thức:
a, ( x3 + 8y3) : (2y+ x)
b, ( x3 + 3x2y+ 3xy2 + y3): (2x+2y)
c, ( 6x5y2 - 9x4y3 + 15x3y4) : 3x3y2
d, (2x3- 21x2 + 67x - 60) : (x-5)
e, ( x4 + 2x3 +x - 25) : (x2 +5)
f, (27x3 -8) : ( 6x + 9x2 +4)
làm tính chia
\(\left[3\left(x-y\right)^4+2\left(x-y\right)^3-5\left(x-y\right)^2\right]:\left(y-x\right)^2\)
gợi ý có thể đặt x-y=z rồi áp dụng qui tắc chia đa thức cho đơn thức
tìm và xác định số hiệu tỷ a,b sao cho : 3x^3+ax^2+bx+9 chia hết cho đa thức x^2-9
B) x^4+ax^33+bx-1 chia hết cho x^2-1
Làm tính chia :
\(\left[3\left(x-y\right)^4+2\left(x-y\right)^3-5\left(x-y\right)^2\right]:\left(y-x\right)^2\)
Gợi ý : Có thể đặt \(x-y=z\) rồi áp dụng quy tắc chia đa thức cho đơn thức
21 tháng 12 2019 lúc 12:54
cho \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)=0
chứng minh rằng: (x2y2+y2z2+z2x2)2=2(x4y4+y4z4+z4x4)