13) để căn thức xác định \(\Rightarrow\dfrac{2x-4}{-2}\ge0\) mà \(-2< 0\Rightarrow2x-4\le0\)
\(\Rightarrow x-2\le0\Rightarrow x\le2\)
14) để căn thức xác định \(\Rightarrow-\dfrac{2}{x-2}\ge0\Rightarrow\dfrac{2}{x-2}\le0\)
mà \(2>0\Rightarrow x-2< 0\Rightarrow x< 2\)
15) để căn thức xác định \(\Rightarrow\dfrac{2\sqrt{15}-\sqrt{59}}{7-x}\ge0\)
Ta có: \(2\sqrt{15}=\sqrt{60}>\sqrt{59}\left(60>59\right)\Rightarrow2\sqrt{15}-\sqrt{59}>0\)
\(\Rightarrow7-x>0\Rightarrow x< 7\)
3) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}1-x\ge0\\3-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le1\\x\le3\end{matrix}\right.\Rightarrow x\le1\)
4) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}15-3x\ge0\\5-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le5\\x\le5\end{matrix}\right.\Rightarrow x\le5\)
5) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}3x-9\ge0\\9-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge3\\x\le9\end{matrix}\right.\Rightarrow3\le x\le9\)
Bài 1:
1) \(\sqrt{2}< \sqrt{3}\)
2) \(\sqrt{3}< \sqrt{10}\)
3) \(2\sqrt{3}>2\sqrt{2}\)
4) \(3\sqrt{3}< 3\sqrt{5}\)
5) \(5\sqrt{2}>3\sqrt{2}\)
6) \(-5\sqrt{3}< -3\sqrt{3}\)

 Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai
Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai








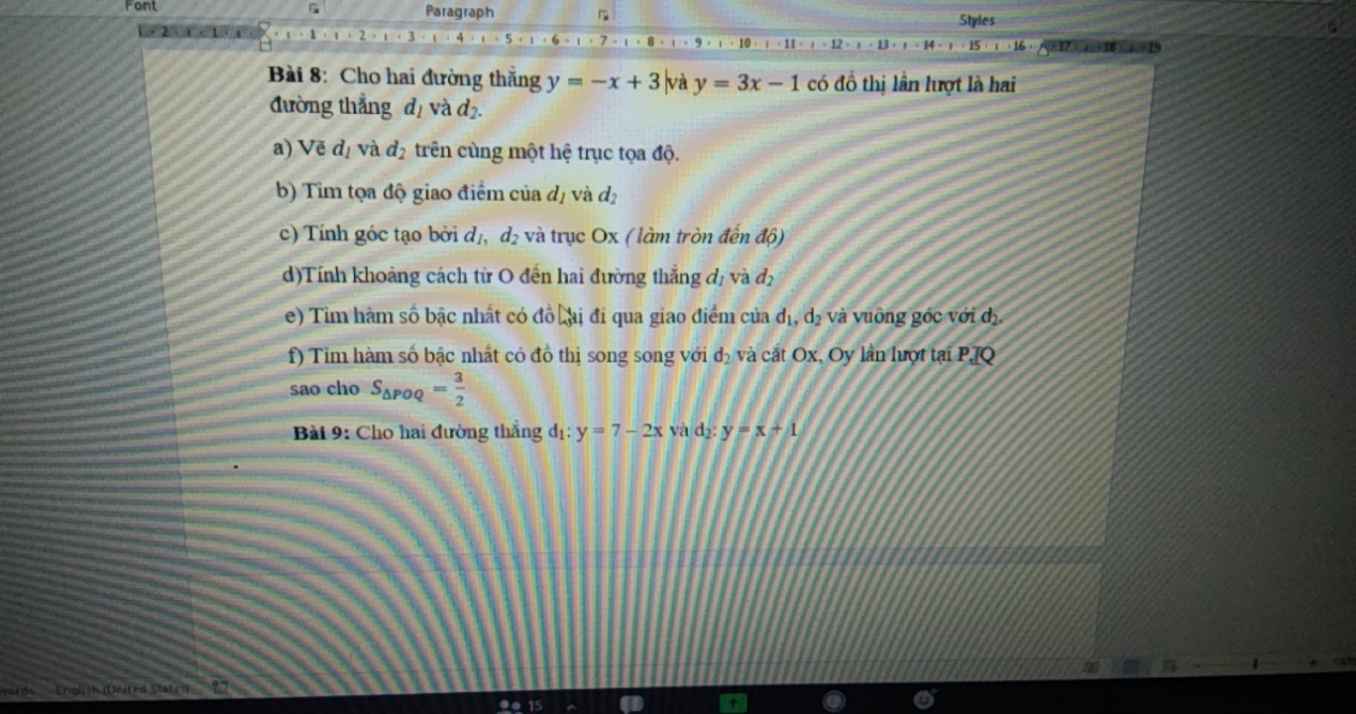
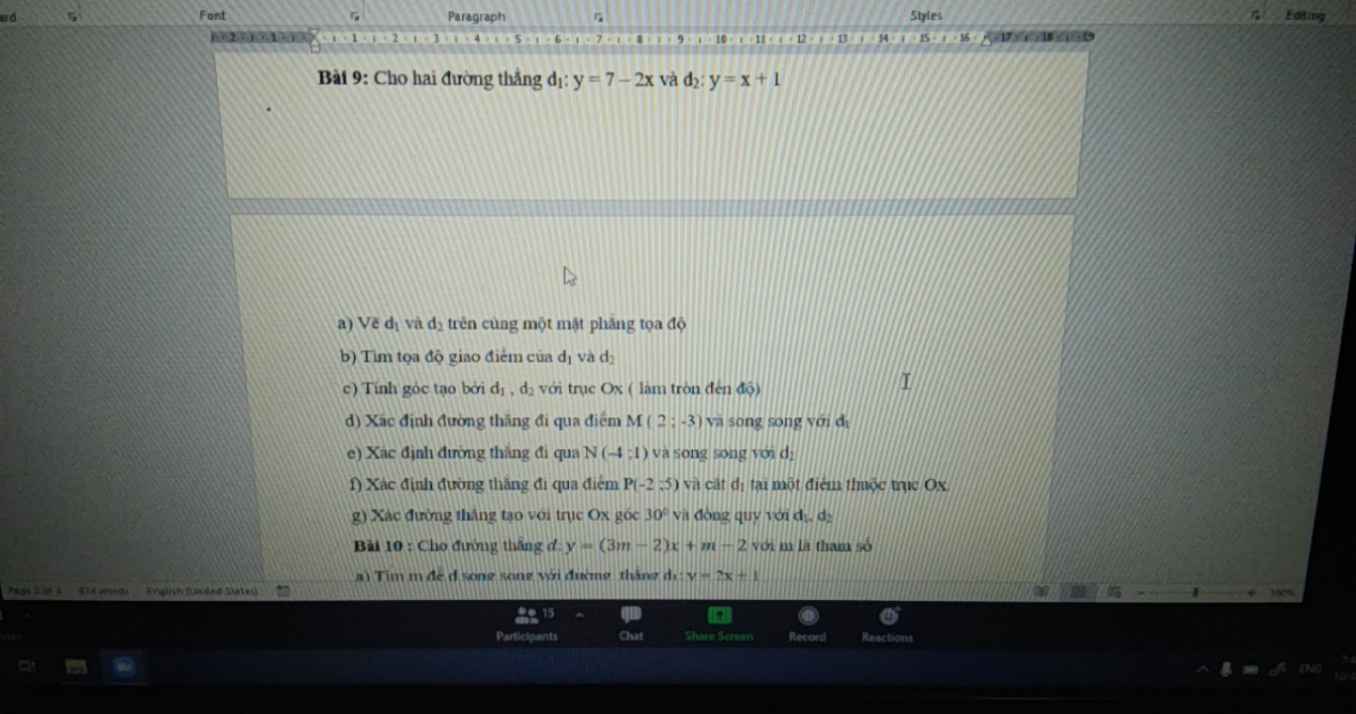






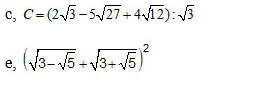
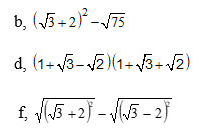 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp


 giúp câu c vs ạ,mik cần gấp
giúp câu c vs ạ,mik cần gấp