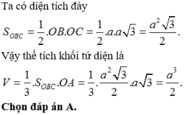Các câu hỏi tương tự
Cho khối tứ diện OABC có OA, OB, OC đôi một vuông góc và OA a, OB b, OC c. Thể tích V của khối tứ diện OABC được tính bởi công thức nào sau đây? A.
V
1
6
a
.
b
.
c
B.
V...
Đọc tiếp
Cho khối tứ diện OABC có OA, OB, OC đôi một vuông góc và OA = a, OB = b, OC = c. Thể tích V của khối tứ diện OABC được tính bởi công thức nào sau đây?
A. V = 1 6 a . b . c
B. V = 1 3 a . b . c
C. V = 1 2 a . b . c
D. V = 3 a . b . c
Cho tứ diện OABC có OAa; OB2a; OC3a đôi một vuông góc với nhau tại O. Lấy M là trung điểm của cạnh AC; N nằm trên cạnh CB sao cho CN2/3 CB. Tính theo a thể tích khối chóp OAMNB A.
2
a
3
B.
a
3
6
C.
2
a
3
3
D. ...
Đọc tiếp
Cho tứ diện OABC có OA=a; OB=2a; OC=3a đôi một vuông góc với nhau tại O. Lấy M là trung điểm của cạnh AC; N nằm trên cạnh CB sao cho CN=2/3 CB. Tính theo a thể tích khối chóp OAMNB
A. 2 a 3
B. a 3 6
C. 2 a 3 3
D. a 3 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):
x
a
+
y
2
a
+
z
3
a
1
(a0) cắt ba trục Ox, Oy, Oz lần lượt tại 3 điểm A, B, C. Tính diện tích V của khối tứ diện OABC A. V
a
3
B. V3...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x a + y 2 a + z 3 a = 1 (a>0) cắt ba trục Ox, Oy, Oz lần lượt tại 3 điểm A, B, C. Tính diện tích V của khối tứ diện OABC
A. V= a 3
B. V=3 a 3
C. V=2 a 3
D. V=4 a 3
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết
O
A
a
,
O
B
2
a
và đường thẳng AC tạo với mặt phẳng
O
B
C
một góc
60
°
.
Thể tích khối tứ diện OABC bằng A.
a
3
3...
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết O A = a , O B = 2 a và đường thẳng AC tạo với mặt phẳng O B C một góc 60 ° . Thể tích khối tứ diện OABC bằng
A. a 3 3 9
B. 3 a 3
C. a 3
D. a 3 3 3
Cho tứ diện ABCD có
A
B
,
A
C
,
A
D
đôi một vuông góc với nhau,
A
B
a
,
A
C
b
,
A
D
c
.
Tính thể tích V của khối tứ diện ABCD theo a, b, c A.
V
a
b
c
2...
Đọc tiếp
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, AAa,
B
A
C
^
30
0
,
A
B
a
3
. Gọi M là trung điểm của BB. Tính theo a thể tích V của khối tứ diện MACC A.
V
a
3
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AA'=a, B A C ^ = 30 0 , A B = a 3 . Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng
60
°
. Tính thể tích V của khối tứ diện ABCD theo a: A.
V
a
3
8
B.
V
a
3
3
16
C.
V...
Đọc tiếp
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 ° . Tính thể tích V của khối tứ diện ABCD theo a:
A. V = a 3 8
B. V = a 3 3 16
C. V = a 3 2 8
D. V = a 3 2 12
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác vuông tại C, BB a, góc
B
A
C
^
60
∘
,
đường thẳng BB tạo với (ABC) một góc
60
∘
,
Hình chiếu vuông góc của B lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A...
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại C, BB' = a, góc B A C ^ = 60 ∘ , đường thẳng BB' tạo với (ABC) một góc 60 ∘ , Hình chiếu vuông góc của B' lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A'.ABC là:
A. 1 208 a 3 .
B. 18 208 a 3 .
C. 9 208 a 3 .
D. 27 208 a 3 .
Cho tứ diện OABC có OA;OB;OC đôi một vuông góc và
O
A
a
,
O
B
b
,
O
C
c
. Tính thể tích khối tứ diện OABC. A. abc B. abc/3 C. abc/6 D. abc/2
Đọc tiếp
Cho tứ diện OABC có OA;OB;OC đôi một vuông góc và O A = a , O B = b , O C = c . Tính thể tích khối tứ diện OABC.
A. abc
B. abc/3
C. abc/6
D. abc/2