Các câu hỏi tương tự
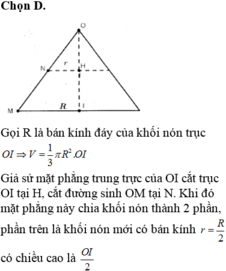
Cho khối nón đỉnh O, trục OI. Mặt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
A. 1 2
B. 1 8
C. 1 4
D. 1 7
Cho khối nón đỉnh O, trục OI. Măt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
A. 1 2
B. 1 8
C. 1 4
D. 1 7
Cho khối nòn đỉnh O, trục OI. Mặt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
A. 1 2
B. 1 8
C. 1 4
D. 1 7
Cho hình nón đỉnh O, I là tâm đường tròn đáy. Mặt trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần chứa đỉnh S và phần không chứa S là: A.
1
8
B.
1
2
C.
1
4
D.
1
7
Đọc tiếp
Cho hình nón đỉnh O, I là tâm đường tròn đáy. Mặt trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần chứa đỉnh S và phần không chứa S là:
A. 1 8
B. 1 2
C. 1 4
D. 1 7
Cho khối nón đỉnh S, trục SI (I là tâm của đáy). Mặt phẳng trung trực của SI chứa khối chóp thành hai phần. Gọi
V
1
là thể tích cảu phần chứa S và
V
2
là thể tích của phần còn lại. Tính
V
1
V
2
? A.
V
1
V...
Đọc tiếp
Cho khối nón đỉnh S, trục SI (I là tâm của đáy). Mặt phẳng trung trực của SI chứa khối chóp thành hai phần. Gọi V 1 là thể tích cảu phần chứa S và V 2 là thể tích của phần còn lại. Tính V 1 V 2 ?
A. V 1 V 2 = 1 4
B. V 1 V 2 = 1 8
C. V 1 V 2 = 1 7
D. V 1 V 2 = 1 2
Một khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng 3 cm2. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 600 chia khối nón thành hai phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm) A. 4,36 cm3 B. 5,37 cm3 C. 5,61 cm3 D. 4,53 cm3
Đọc tiếp
Một khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng 3 cm2. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 600 chia khối nón thành hai phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm)
A. 4,36 cm3
B. 5,37 cm3
C. 5,61 cm3
D. 4,53 cm3
Trong không gian Oxyz, cho hình nón có đỉnh I thuộc mặt phẳng
P
:
2
x
-
y
-
2
z
-
7
0
và hình tròn đáy nằm trên mặt phẳng
R
:
2
x
-
y
-
2
z
+
8
0
.
Mặt phẳng (Q) đi qua điểm
A
0
;...
Đọc tiếp
Trong không gian Oxyz, cho hình nón có đỉnh I thuộc mặt phẳng P : 2 x - y - 2 z - 7 = 0 và hình tròn đáy nằm trên mặt phẳng R : 2 x - y - 2 z + 8 = 0 . Mặt phẳng (Q) đi qua điểm A 0 ; - 2 ; 0 và vuông góc với trục của hình nón chia hình nón thành hai phần có thể tích lần lượt là V 1 và V ( V 1 là thể tích của phần chứa đỉnh I ). Biết rằng biểu thức S = V 2 + 78 V 1 3 đạt giá trị nhỏ nhất khi V 1 = a , V 2 = b . Khi đó tổng a 2 + b 2 bằng
A. 2031 π 2
B. 377 3
C. 52 3 π 2
D. 2031
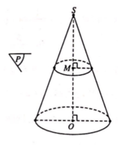
Cắt một khối nón tròn xoay có thể tích V thành hai phần bằng một mặt phẳng (P) song song với đáy (như hình vẽ). Tính thể tích khối nón cụt tạo thành, biết mặt phẳng (P) đi qua trung điểm của đường cao SO. A.
7
8
V
B.
3
8
V
C.
5
8...
Đọc tiếp
Cắt một khối nón tròn xoay có thể tích V thành hai phần bằng một mặt phẳng (P) song song với đáy (như hình vẽ). Tính thể tích khối nón cụt tạo thành, biết mặt phẳng (P) đi qua trung điểm của đường cao SO.
A. 7 8 V
B. 3 8 V
C. 5 8 V
D. 6 8 V
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của hình nón đỉnh S đáy là hình tròn tâm O' là. (biết thể tích của nó bằng 1/8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O).
A. h=5
B. h=10
C. h=20
D. h=40