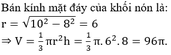Các câu hỏi tương tự
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Cho hình nón có thể tích bằng 12
π
và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương. A. 4 B. 3. C. 6 D. 5
Đọc tiếp
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Cho khối nón có chiều cao bằng 24cm, độ dài đường sinh bằng 26cm. Tính thể tích V của khối nón tương ứng. A.
V
800
π
c
m
3
B.
V
1600
π
c
m
3
C.
V
1600
π
3
c
m
3
D. ...
Đọc tiếp
Cho khối nón có chiều cao bằng 24cm, độ dài đường sinh bằng 26cm. Tính thể tích V của khối nón tương ứng.
A. V = 800 π c m 3
B. V = 1600 π c m 3
C. V = 1600 π 3 c m 3
D. V = 800 π 3 c m 3
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón . Thể tích V của khối nón bằng A.
V
1
3
π
R
2
h
B.
V
π
R
2
h
C.
V
π
R...
Đọc tiếp
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón . Thể tích V của khối nón bằng
A. V = 1 3 π R 2 h
B. V = π R 2 h
C. V = π R 2 l
D. V = 1 3 π R 2 l
Trong các khối trụ có cùng diện tích toàn phần bằng
π
. Gọi
τ
là khối trụ có thể tích lớn nhất, chiều cao của
τ
bằng A.
π
3
B.
6
3
C.
6
6
D.
π
3
4
Đọc tiếp
Trong các khối trụ có cùng diện tích toàn phần bằng π . Gọi τ là khối trụ có thể tích lớn nhất, chiều cao của τ bằng
A. π 3
B. 6 3
C. 6 6
D. π 3 4
Trong các khối trụ có cùng diện tích toàn phần bằng
π
, gọi (T) là khối trụ có thể tích lớn nhất, chiều cao của (T)bằng A.
3
4
B.
6
3
C.
6
6
D.
π
3
4
Đọc tiếp
Trong các khối trụ có cùng diện tích toàn phần bằng π , gọi (T) là khối trụ có thể tích lớn nhất, chiều cao của (T)bằng
A. 3 4
B. 6 3
C. 6 6
D. π 3 4
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng
60
°
. Thể tích của khối nón đã cho là A.
πa
3
3
3
B.
πa
3
3
3
C.
πa
3...
Đọc tiếp
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng 60 ° . Thể tích của khối nón đã cho là
A. πa 3 3 3
B. πa 3 3 3
C. πa 3 2 3
D. πa 3 3
Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là
R
17
và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón A.
5
12
πR
3
B.
1
3
πR
3
C.
4
3
πR...
Đọc tiếp
Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là R 17 và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón

A. 5 12 πR 3
B. 1 3 πR 3
C. 4 3 πR 3
D. 5 6 πR 3
Cho hai khối nón (
N
1
),(
N
2
) . Chiều cao khối nón (
N
2
) bằng hai lần chiều cao khối nón (
N
1
) và đường sinh khối nón (
N
2
) bằng hai lần đường sinh khối nón (
N
1
). Gọi
V
1
,...
Đọc tiếp
Cho hai khối nón ( N 1 ),( N 2 ) . Chiều cao khối nón ( N 2 ) bằng hai lần chiều cao khối nón ( N 1 ) và đường sinh khối nón ( N 2 ) bằng hai lần đường sinh khối nón ( N 1 ). Gọi V 1 , V 2 lần lượt là thể tích hai khối nón ( N 1 ), ( N 2 ). Tỉ số bằng V 1 V 2
A. 1 6
B. 1 8
C. 1 16
D. 1 4