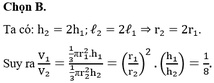Các câu hỏi tương tự
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón . Thể tích V của khối nón bằng A.
V
1
3
π
R
2
h
B.
V
π
R
2
h
C.
V
π
R...
Đọc tiếp
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón . Thể tích V của khối nón bằng
A. V = 1 3 π R 2 h
B. V = π R 2 h
C. V = π R 2 l
D. V = 1 3 π R 2 l
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai A.
V
1
3
πrh
B.
l
2
h...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A. V = 1 3 πrh
B. l 2 = h 2 + r 2
C. S t p = πr 1 + r
D. S x q = πrl
Cho hình nón đỉnh O, chiều cao h. Một khối nón (N) có đỉnh và đáy lần lượt là tâm của đáy và một thiết diện song song với đáy của hình nón đã cho. Để thể tích của khối nón (N) lớn nhất thì chiều cao của khối nón này bằng bao nhiêu? A.
h
3
B.
h
2
C.
2
h
3
D.
h
3...
Đọc tiếp
Cho hình nón đỉnh O, chiều cao h. Một khối nón (N) có đỉnh và đáy lần lượt là tâm của đáy và một thiết diện song song với đáy của hình nón đã cho. Để thể tích của khối nón (N) lớn nhất thì chiều cao của khối nón này bằng bao nhiêu?
A. h 3
B. h 2
C. 2 h 3
D. h 3 3
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón. Thể tích của khối nón là V. Chọn đẳng thức đúng. A.
π
R
2
l
B.
1
3
π
R
2
l
C.
1
3
π
R...
Đọc tiếp
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón. Thể tích của khối nón là V. Chọn đẳng thức đúng.
A. π R 2 l
B. 1 3 π R 2 l
C. 1 3 π R 2 h
D. π R 2 h
Cho khối nón có độ lớn ở đỉnh là
π
3
. Một khối cấu
S
1
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các dường sinh của nón và với
S
1
,
S
3
là khối tiếp xúc với tất cả các đường sinh của nón với
S
2...
Đọc tiếp
Cho khối nón có độ lớn ở đỉnh là π 3 . Một khối cấu S 1 nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các dường sinh của nón và với S 1 , S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 2 ; . . . ; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , . . . , V n - 1 , V n lần lượt là thể tích của khối cấu S 1 , S 2 , . . . , S n - 1 , S và V là thể tích của khối nón. Tính giá trị của biểu thức l i m n → ∞ = V 1 + V 2 + . . . + V n V
A. 3 5
B. 6 13
C. 7 9
D. 1 2
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu (
S
1
) nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối tiếp xúc với tất cả các đường sinh của nón với
S
2
;…;...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 2 ;…; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , … , V n - 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , … , S n và V là thể tích của khối nón. Tính giá trị của biểu thức T = lim n → + ∞ V 1 + V 2 + . . . + V n V
A. 3 5
B. 6 13
C. 7 9
D. 1 2
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu
S
1
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
2
;...;
S...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu S 1 nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 2 ;...; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , ... V n − 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , ... , S n − 1 , S n và V là thể tích của khối nón. Tính giá trị biểu thức T = lim n → + ∞ V 1 + V 2 + ... + V n V
A. 7 9 .
B. 1 2 .
C. 6 13 .
D. 3 5 .
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu
S
1
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối tiếp xúc với tất cả các đường sinh của nón và với...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu S 1 nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón và với S 2 ; . . . ; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , ... , V n − 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , ... , S n − 1 , S n và V là thể tích của khối nón. Tính giá trị biểu thức T = lim n → + ∞ V 1 + V 2 + ... + V n V .
A. 7 9
B. 1 2
C. 6 13
D. 3 5
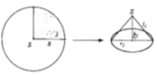
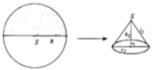
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đâyCách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón
N
1
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón
N
2
Gọi
V
1
,
V
2...
Đọc tiếp
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đây
Cách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón N 1
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón N 2
Gọi V 1 , V 2 lần lượt là thể tích của khối nón N 1 và khối nón N 2 . Tính V 1 V 2
A. V 1 V 2 = 9 3 4 2
B. V 1 V 2 = 3 3 2 2
C. V 1 V 2 = 7 2 3
D. V 1 V 2 = 9 7 8 3