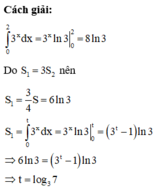Các câu hỏi tương tự
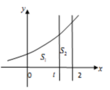
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
, y0, x0, x2. Đường thẳng x1 (0t2) chia (H) thành hai phần có diện tích
S
1
và
S
2
(như hình vẽ). Tìm t để
S
1
3
S
2
A.
t
log
3
5...
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y=0, x=0, x=2. Đường thẳng x=1 (0<t<2) chia (H) thành hai phần có diện tích S 1 và S 2 (như hình vẽ). Tìm t để S 1 = 3 S 2
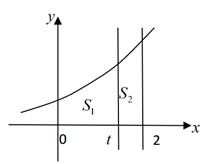
A. t = log 3 5
B. t = log 3 2
C. t = log 3 35
D. t = log 3 7
Cho hình thang cong (H) giới hạn bởi các đưởng
y
2
x
, y 0, x 0, x 4.Đường thẳng x 1(0 a 4) chia hình (H) thànhhai phần có diện tích là
S
1
và
S
2
như hình vẽ bên.Tìm a để
S
2
4
S
1
A.
a
3
B.
a
log
2...
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đưởng y = 2 x , y = 0, x = 0, x = 4.
Đường thẳng x = 1(0 < a < 4) chia hình (H) thành
hai phần có diện tích là S 1 và S 2 như hình vẽ bên.
Tìm a để S 2 = 4 S 1
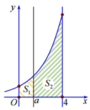
A. a = 3
B. a = log 2 13
C. a = 2
D. a = log 2 16 5
Cho hình thang cong
H
giới hạn bởi các đưởng
y
2
x
, y 0, x 0, x 4. Đường thẳng chia hình
H
thành hai phần có diện tích là
S
1
và
S
2
như hình vẽ bên. Tìm a để
S
2
4
S
1
A. a 3 B.
a
log...
Đọc tiếp
Cho hình thang cong H giới hạn bởi các đưởng y = 2 x , y = 0, x = 0, x = 4. Đường thẳng chia hình H thành hai phần có diện tích là S 1 và S 2 như hình vẽ bên. Tìm a để S 2 = 4 S 1
A. a = 3
B. a = log 2 13
C. a = 2
D. a = log 2 16 5
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1, y=0, x=1, x=t (t>1). Tìm t để S(t)=10
A. t=4
C. t=13
C. t=3
D. t=4
Cho hình thang cong (H) giới hạn bởi các đường
y
e
x
,
y
0
,
x
0
và x ln8 Đường thẳng x k (0 k ln8) chia (H) thành hai phần có diện tích là S1 và S2. Tìm k để S1 S2? A.
k
...
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = e x , y = 0 , x = 0 và x = ln8 Đường thẳng x = k (0 < k < ln8) chia (H) thành hai phần có diện tích là S1 và S2. Tìm k để S1 = S2?
A. k = ln 9 2 .
B. k = ln4.
C. k = 2 3 ln 4 .
D. k = ln5.
Cho hình thang cong (H) giới hạn bởi các đường
y
e
x
, y 0, x -2, x 2. Đường thẳng
x
k
−
2
k
2
chia (H) thành hai phần
S
1
,
S...
Đọc tiếp
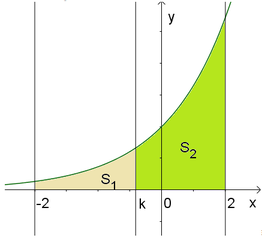
Cho hình thang cong (H) giới hạn bởi các đường y = e x , y = 0, x = -2, x= 2. Đường thẳng x = k − 2 < k < 2 chia (H) thành hai phần S 1 , S 2 như hình vẽ dưới. Cho S 1 và S 2 quay quanh trục Ox ta thu được hai khối tròn xoay có thể tích lần lượt là V 1 và V 2 . Xác định k để V 1 = V 2 .
A. k = 1 2 ln e 4 − e − 4 2
B. k = 1 2 ln e 2 + e − 2 2
C. k = 1 2 ln e 4 + e − 4 2
D. k = ln e 4 + e − 4 2
Cho hình thang cong (H) giới hạn bởi các đường
y
1
x
,
x
1
2
,
x
2
và trục hoành. Đường thẳng x k (
1
2
k 2) chia (H) thành hai phần có diện tích là
S
1
và
S
2
như hình vẽ bên. Tìm tất cả gi...
Đọc tiếp
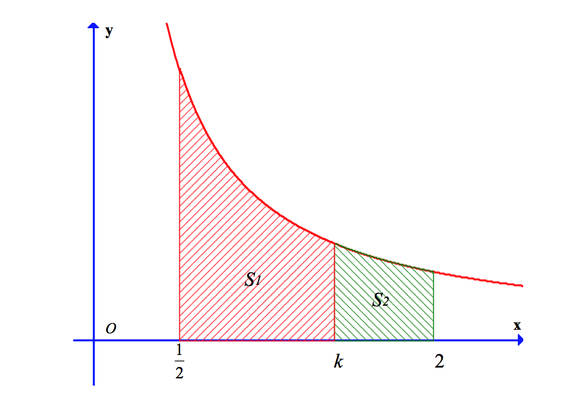
Cho hình thang cong (H) giới hạn bởi các đường y = 1 x , x = 1 2 , x = 2 và trục hoành. Đường thẳng x = k ( 1 2 < k <2) chia (H) thành hai phần có diện tích là S 1 và S 2 như hình vẽ bên. Tìm tất cả giá trị thực của k để S 1 = 3 S 2 .
A. k = 2
B. k = 1
C. k = 7 5
D. k = 3
Cho hình thang cong (H) giới hạn bởi các đường
y
1
x
,
x
1
2
,
x
2
và trục hoành. Đường thẳng
x
k
,
1
2
k
2
chia (H) thành hai phần có diện tích là...
Đọc tiếp
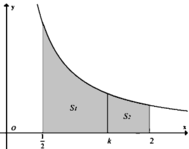
Cho hình thang cong (H) giới hạn bởi các đường y = 1 x , x = 1 2 , x = 2 và trục hoành. Đường thẳng x = k , 1 2 < k < 2 chia (H) thành hai phần có diện tích là S 1 và S 2 như hình vẽ dưới đây. Tìm tất cả giá trị thực của k để S 1 = 3 S 2
A. k = 2
B. k = 1
C. k = 7 5
D. k = 3
Xét hình phẳng (H)được giới hạn bởi các đường thẳng
y
0,
x
0
và đường
y
x
+
3
2
. Gọi
A
0
;
9
,
B
b
;
0
−...
Đọc tiếp
Xét hình phẳng (H)được giới hạn bởi các đường thẳng y = 0, x = 0 và đường y = x + 3 2 . Gọi A 0 ; 9 , B b ; 0 − 3 < b < 0 . Tìm giá trị của b để đoạn thẳng AB chia (H) thành hai phần có diện tích bằng nhau?
A. b = − 2
B. b = − 1 2
C. b = − 1
D. b = − 3 2