Đáp án D
![]()
Do đó
![]()
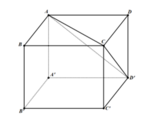
Tứ diện DACD’ vuông tại D nên ta có:
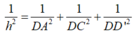


Đáp án D

![]()
Do đó
![]()
Tứ diện DACD’ vuông tại D nên ta có:
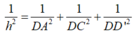


Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính khoảng cách từ M đến mặt phẳng (AB’C).
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = AB = a, AD = 2a. Tính khoảng cách h từ A tới mặt phẳng (B’D’C)
A. h = a
B. h = 2 a 3
C. h = 3 a 2
D. h = 4 a 3
Cho hình hộp chữ nhật ABCD.A'B'C'D có AB = AA' = 2a, AD = a. Tính khoảng cách h từ C' tới mặt phẳng (A'BD)
A. h = 2 a 3
B. h = a 3
C. h = 4 a 6
D. h = 3 a 4
Câu 21: Cho khối hộp chữ nhật ABCD.A'B'C'D'. Biết AC=5, AB'=7, AD'=8. Tính thể tích khối hộp chữ nhật này?
Câu 36: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, \(AD=a\sqrt{3}\). SA\(\perp\)(ABCD), SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với cạnh bên SC, cắt các cạnh bên SB,SC,SD lần lượt tại E,F,H. Tính thể tích khối chóp S.AEFH?
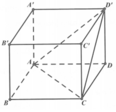
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = a 2 , AA' = a 3 .
Gọi a là góc giữa 2 mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ).
Giá trị tana bằng:
A. 2
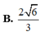
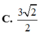
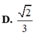
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB = AD = a, AA' = a 2 . Tính khoảng cách h từ D xuống mặt phẳng (BCD').
A. h = a 2 3
B. h = a 2 3
C. h = a 3
D. h = a 2
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC = a 3 , AD' = 2a, AB' = a 5 . Tính thể tích V của hình hộp.
A. V = 2 a 3 15
B. V = a 3 15 3
C. V = a 3 6
D. V = 3 a 3
Cho lăng trụ đứng ABCA1B1C1 có AB = a, AC = 2a, AA = 2a\(\sqrt{5}\) và \(\widehat{BAC}=120^0\) Gọi M là trung điểm của CC1. CM \(MB\perp MA_1\) và tính khoảng cách từ điểm A đến mặt phẳng \(\left(A_1BM\right)\)