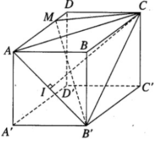
Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)
Khi đó
![]()
Vì AC 2 = B ' C 2 = 5 a 2 nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.
Ta có:
![]()
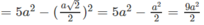
Do đó
![]()
Từ đó suy ra
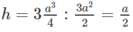

Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)
Khi đó
![]()
Vì AC 2 = B ' C 2 = 5 a 2 nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.
Ta có:
![]()
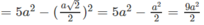
Do đó
![]()
Từ đó suy ra
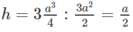
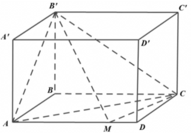
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính thể tích khối chóp M.AB’C
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a; BC = 2a; AA’= a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính thể tích khối chóp M.AB’C.
A. V = a 3 2
B. V = a 3 4
C. V = 3 a 3 4
D. V = 3 a 3 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=AA’=a, AC=2a. Khoảng cách từ điểm D đến mặt phẳng (ACD') là
A. a 3 3
B. a 5 5
C. a 10 5
D. a 21 7
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm I trên cạnh AD sao cho AI = 3ID. Tính thể tích của khối chóp B’.IAC.
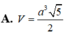
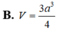
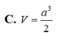
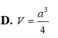
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = AB = a, AD = 2a. Tính khoảng cách h từ A tới mặt phẳng (B’D’C)
A. h = a
B. h = 2 a 3
C. h = 3 a 2
D. h = 4 a 3
Cho hình hộp chữ nhật ABCD.A'B'C'D có AB = AA' = 2a, AD = a. Tính khoảng cách h từ C' tới mặt phẳng (A'BD)
A. h = 2 a 3
B. h = a 3
C. h = 4 a 6
D. h = 3 a 4
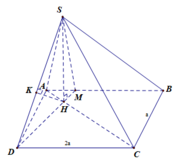
Cho hình chóp S.ACBD có đáy ABCD là hình chữ nhật, biết AB = 2a, AD = a. Trên cạnh AB lấy điểm M sao cho A M = a 2 , Cạnh AC cắt MD tại H. Biết SH vuông gốc với mặt phẳng (ABCD) và SH = a. Khoảng cách giữa hai đường thẳng SD và AC
A. a 3
B. 2 a 5
C. 2 a 3
D. a 2
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB = AD = a, AA' = a 2 . Tính khoảng cách h từ D xuống mặt phẳng (BCD').
A. h = a 2 3
B. h = a 2 3
C. h = a 3
D. h = a 2
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2