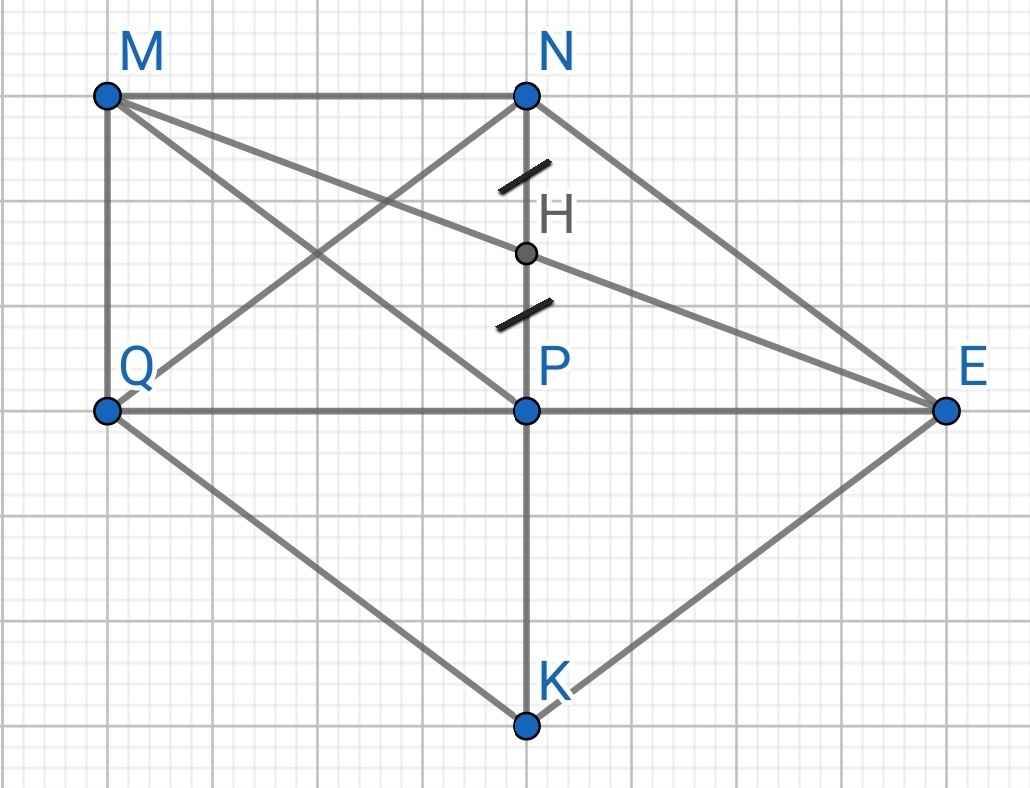
 a) Do MNPQ là hình chữ nhật (gt)
a) Do MNPQ là hình chữ nhật (gt)
⇒ NP ⊥ PQ
⇒ NP ⊥ PE
Xét hai tam giác vuông: ∆NHM và ∆PHE có:
NH = HP (gt)
NHM = PHE (đối đỉnh)
⇒ ∆NHM = ∆PHE (cạnh góc vuông - góc nhọn kề)
b) Do ∆NHM = ∆PHE (cmt)
⇒ MN = PE (hai cạnh tương ứng)
Do MNPQ là hình chữ nhật (gt)
⇒ MN // PQ
⇒ MN // PE
Tứ giác MNEP có:
MN // PE (cmt)
MN = PE (cmt)
⇒ MNEP là hình bình hành
c) Do MNPQ là hình chữ nhật
⇒ MN = PQ
Mà MN = PE (cmt)
⇒ PQ = PE
⇒ P là trung điểm của QE
Do N và K đối xứng với nhau qua P (gt)
⇒ P là trung điểm của NK
Do NP ⊥ PQ (cmt)
⇒ NK ⊥ QE
Tứ giác QNEK có:
P là trung điểm của QE (cmt)
P là trung điểm của NK (cmt)
⇒ QNEK là hình bình hành
Mà NK ⊥ QE (cmt)
⇒ QNEK là hình thoi
a. Ta có:
- H là trung điểm của NP, nên NH = HM.
- E là giao điểm của MH và PQ, nên HE = EP.
- Ta cũng có NM = NP (do H là trung điểm của NP).
Vậy, ta có NHM ≅ PHE theo nguyên tắc cạnh - cạnh - cạnh.
b. Ta có:
- M là trung điểm của NE (do H là trung điểm của NP).
- H là trung điểm của NP (do H là trung điểm của NP).
Vậy, ta có MNEP là hình bình hành theo định nghĩa của hình bình hành.
c. Gọi K là điểm đối xứng của N qua P. Ta cần chứng minh tứ giác QNEK là hình thoi.
- Ta có NP = NK (do K là điểm đối xứng của N qua P).
- Ta cũng có NQ = NE (do MNEP là hình bình hành).
- Vì NP = NK và NQ = NE, nên ta có NPQ ≅ NKE theo nguyên tắc cạnh - cạnh - cạnh.
- Do đó, góc NQK = góc NEK.
- Nhưng góc NEK = góc NHE (do NHM ≅ PHE).
- Vậy, góc NQK = góc NHE.
- Ta cũng có góc QNK = góc ENH (do NHM ≅ PHE).
- Vậy, tứ giác QNEK có hai cặp góc đối nhau bằng nhau, nên QNEK là hình thoi theo định nghĩa của hình thoi.
a: Xét ΔHPE vuông tại P và ΔHNM vuông tại N có
HP=HN
\(\widehat{PHE}=\widehat{NHM}\)
Do đó: ΔHPE=ΔHNM
b: ΔHPE=ΔHNM
=>PE=NM
MN//QP
P\(\in\)QE
Do đó: MN//PE
Xét tứ giác MNEP có
MN//EP
MN=EP
Do đó: MNEP là hình bình hành
c: Ta có: MN=PQ(MNPQ là hình chữ nhật)
mà MN=PE
nên PQ=PE
=>P là trung điểm của QE
Xét tứ giác QNEK có
P là trung điểm chung của QE và NK
Do đó: QNEK là hình bình hành
Hình bình hành QNEK có QE\(\perp\)NK tại P
nên QNEK là hình thoi















