$#Shả$
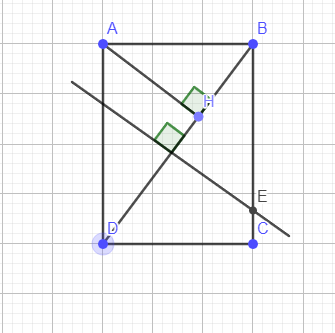
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.














