Các câu hỏi tương tự
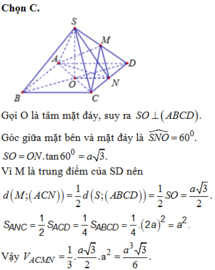
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng
60
°
.
Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD,DC. Thể tích khối tứ diện ACMN là A.
a
3
2
4
B.
a
3
8
C.
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng 60 ° . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD,DC. Thể tích khối tứ diện ACMN là
A. a 3 2 4
B. a 3 8
C. a 3 3 6
D. a 3 2 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng
60
0
. Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là A.
a
3
2
4
.
B.
a
3
8...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 0 . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
A. a 3 2 4 .
B. a 3 8 .
C. a 3 3 6 .
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
trong đó
H
1
chứa điểm C. Thể tích của khối là A. ...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 trong đó H 1 chứa điểm C. Thể tích của khối là
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
. Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
, trong đó
H
1
chứa điểm C. Thể t...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 , trong đó H 1 chứa điểm C. Thể tích của khối H 1 là:
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật, cạnh
A
B
a
,
A
D
2
a
,
cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa cạnh SD và mặt phẳng đáy bằng
60
o
. Thể tích V của khối chóp S.ABCD là A.
V
2
a
3...
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật, cạnh A B = a , A D = 2 a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa cạnh SD và mặt phẳng đáy bằng 60 o . Thể tích V của khối chóp S.ABCD là
A. V = 2 a 3 3 .
B. V = 4 a 3 3 .
C. V = a 3 3 .
D. V = 4 a 3 3 .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc
60
°
. Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó A.
1
5
B.
7
3
. C.
1
7
D. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó
A. 1 5
B. 7 3 .
C. 1 7
D. 7 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây? A.
x
2
+
2
x
y
-
y
2
160
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây?
A. x 2 + 2 x y - y 2 > 160
B. x 2 - 2 x y + 2 y 2 < 109
C. x 2 + x y - y 4 < 145
D. x 2 - x y + y 4 > 125
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc
60
∘
. Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V A.
V
7
6
a
3
36
B.
V...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc 60 ∘ . Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V
A. V = 7 6 a 3 36
B. V = 7 6 a 3 72
C. V = 5 6 a 3 72
D. V = 5 6 a 3 36
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . SA vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy bằng
60
0
. Gọi M, N lần lượt là trung điểm của SC và SD . Tính thể tích của khối chóp S.AMN A.
V
S
.
A
M
N
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . SA vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy bằng 60 0 . Gọi M, N lần lượt là trung điểm của SC và SD . Tính thể tích của khối chóp S.AMN
A. V S . A M N = a 3 3 12
B. V S . A M N = a 3 3 24
C. V S . A M N = a 3 3 3
D. V S . A M N = a 3 3 6