Question

cho hình chóp SABCD,đáy là hình bình hành tâm O ,các tam giác SAD và ABC đều cân tại A . Gọi AE,AF là các đường phân giác trong của tam giác ACD và SAB . chứng minh EF//(SAD)

Answer 1

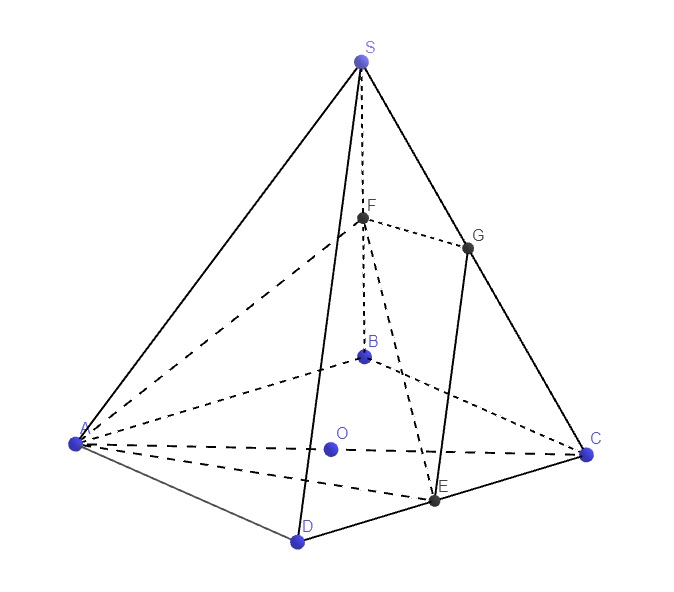
Qua E kẻ đường thẳng song song SD cắt SC tại G \(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}\) (Talet)

Mặt khác theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\Rightarrow\dfrac{GC}{GS}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\) (do AC=AB và AD=SA)

Theo định lý phân giác: \(\dfrac{AB}{SA}=\dfrac{FB}{FS}\Rightarrow\dfrac{GC}{GS}=\dfrac{FB}{FS}\Rightarrow FG||BC\Rightarrow FG||AD\)

\(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||SAD\)

Answer 2