Bạn coi lại đề, sao lại có 2 cái AF là đường cao của 2 tam giác khác nhau thế kia?
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
CHO HÌNH CHÓP SABCD CÓ ĐÁY ABCD LÀ HÌNH CHỮ NHẬT. SA VUÔNG GÓC VỚI ABCD KẺ ĐƯỜNG CAO AM CỦA TAM GIÁC SAB CHỨNG MINH AM VUÔNG GÓC VỚI SBC
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.Hai mặt phẳng (SAB) và (SBC) vuông góc vì. A. Góc của (SAB) và (SBC) là góc ABC và bằng
90
o
. B. Góc của (SAB) và (SBC) là góc BAD và bằng
90
o
. C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC) D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
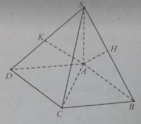
A. Góc của (SAB) và (SBC) là góc ABC và bằng 90 o .
B. Góc của (SAB) và (SBC) là góc BAD và bằng 90 o .
C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)
D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.Hai mặt phẳng (SAC) và (AHK) vuông góc vì: A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK) C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK) D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
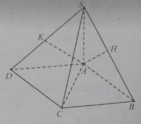
A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)
B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)
C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)
D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)
cho hình chóp S.ABCD, đáy là hình vuông,cạnh a. tâm giác SAB và tam giác SAC vuông tại A. góc giữa SC và(ABCD) bằng 30 độ.
a) chứng minh SA vuông góc với (ABCD)
b)cho AH là đường cao tâm giác SAB, chứng minh AH vuông góc với SC
c)góc giữa SC và (SAB)
Cho hình chóp SABCD đáy là hình vuông cạnh a. Tam giác SAB đều. (SAB) vuông góc với (ABCD) a)(SBC) và (ABCD) b)(SCD) và (ABCD) c)(SAD) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc (ABCD). AH, AK lần lượt là đường cao của tam giác SAB, SAD.
a/ C/m: CD vuông góc SD và AK vuông góc SC.
b/ C/m: SC vuông góc (AHK).
c) Tính góc giữa SO với (ABCD)
d) Tính góc giữa SO với (SAB)
e) Tính khoảng cách từ B đến (SCD)
f) Tính khoảng cách từ H đến (SAC)
cho hình chóp SABCD đáy là hình vuông cạnh 2a. (SAB) vuông góc (ABCD). Tam giác SAB là tam giác cân tại S. Tính thể tích SABCD biết a)Góc giữa SA và đáy là alpha biết tan alpha=2 b)Góc giữa SC và đáy là alpha biết tan alpha= căn 5 c)Góc giữa (SCD) và (ABCD) là alpha biết tan alpha=3
Cho hình chóp SABCD có SA vuông góc với (ABCD) ; đáy ABCD là hình thang vuông tai A và D, AD=DC =a , AB= 2a, SA = a✓3
@) CM CD vuong với (SAD)
B) CM (SAC) vuông voi (SBC)
C) tính góc giua SB và (ABCD) goc giữa SC va (SAB)












