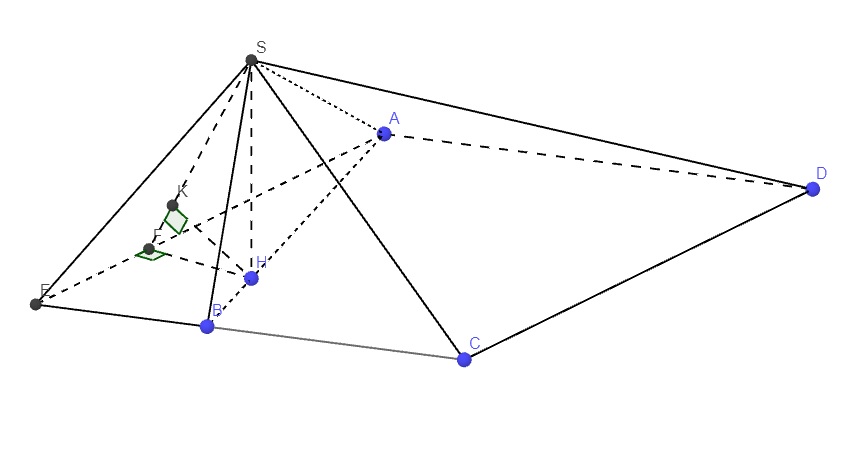
\(SA=\sqrt{AB^2-SB^2}=a\sqrt{3}\)
Từ S kẻ \(SH\perp AB\Rightarrow SH=\dfrac{SA.SB}{AB}=\dfrac{a\sqrt{3}}{2}\)
\(BH=\sqrt{SB^2-SH^2}=\dfrac{a}{2}\) \(\Rightarrow AH=\dfrac{3a}{2}=\dfrac{3}{4}AB\)
Qua A kẻ đường thẳng song song CD cắt BC tại E \(\Rightarrow ADCE\) là hbh nên \(CE=AD=3a\)
\(\Rightarrow BE=CE-BC=2a\Rightarrow\dfrac{CE}{BE}=\dfrac{3}{2}\)
\(\Rightarrow d\left(C;\left(SEA\right)\right)=\dfrac{3}{2}d\left(B;\left(SAE\right)\right)\)
\(BA=\dfrac{4}{3}HA\Rightarrow d\left(B;\left(SEA\right)\right)=\dfrac{4}{3}d\left(H;\left(SAE\right)\right)\)
\(\Rightarrow d\left(SA;DC\right)=d\left(C;\left(SEA\right)\right)=2d\left(H;\left(SAE\right)\right)\)
Từ H kẻ \(HF\perp AE\), từ H kẻ \(HK\perp SF\)
\(HF=AH.sin\widehat{EAB}=AH.\dfrac{EB}{\sqrt{EB^2+AB^2}}=\dfrac{3a\sqrt{2}}{8}\)
\(D\left(SA;DC\right)=2HK=2.\dfrac{HF.SH}{\sqrt{HF^2+SH^2}}=\dfrac{3a\sqrt{11}}{11}\)