Question

Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB=a, AD=2a. Mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy. Gọi H là hình chiếu vuông góc của A trên SD. Tính d(AH,SC), biết AH = a

Answer 1

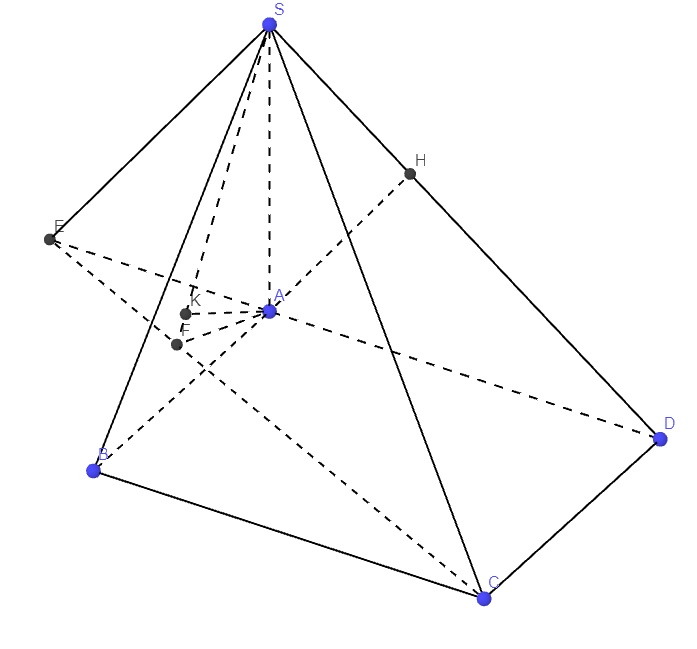
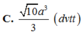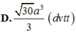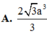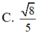Giả thiết suy ra \(SA\perp\left(ABCD\right)\)

Qua S kẻ đường thẳng song song AH cắt AD kéo dài tại E

Từ A kẻ \(AF\perp CE\), kẻ \(AK\perp SFF\Rightarrow AK=d\left(AH;SC\right)\)

\(SA=\dfrac{AD.AH}{\sqrt{AD^2-AH^2}}=\dfrac{2a\sqrt{3}}{3}\) ; \(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{3}}{3}\) 

\(DH=\dfrac{AH^2}{SH}=a\sqrt{3}\)

Talet: \(\dfrac{AE}{AD}=\dfrac{SH}{DH}=\dfrac{1}{3}\Rightarrow AE=\dfrac{2a}{3}\)

\(AF=AE.sinE=AE.\dfrac{CD}{\sqrt{CD^2+DE^2}}=\dfrac{2a\sqrt{73}}{73}\)

\(AK=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=\dfrac{a\sqrt{19}}{19}\)

Số xấu quá, ko biết có tính nhầm đâu ko

Answer 2