Chọn D.
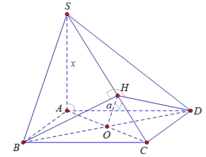
- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
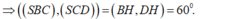
- Có 2 trường hợp xảy ra:
TH1:
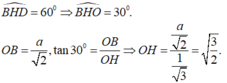
- Xét hai tam giác đồng dạng SAC và OHC ta có

TH2:
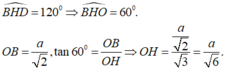
- Xét hai tam giác đồng dạng SAC và OHC ta có:
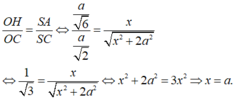
Chọn D.

- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
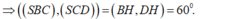
- Có 2 trường hợp xảy ra:
TH1:
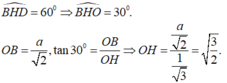
- Xét hai tam giác đồng dạng SAC và OHC ta có

TH2:
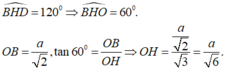
- Xét hai tam giác đồng dạng SAC và OHC ta có:
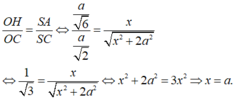
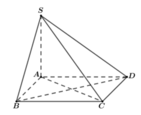
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = x và vuông góc với đáy (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) hợp với nhau góc 60 o
A. x = a 2
B. x = a
C. x = 3 a 2
D. x = 2a
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, \(AB=a;AD=a\sqrt{3}\), cạnh bên SA vuông góc (ABCD). Biết mp(SBC) tạo với đáy một góc 60 độ. Tính \(cos\widehat{\left(SBC\right);\left(SCD\right)}\)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB= BC= a AD=2 a ; SA vuông góc với mặt phẳng (ABCD) và SA =2a . Gọi M là một điểm trên cạnh AB; α là mặt phẳng đi qua M, vuông góc với AB. Đặt x= AM (0<x<a).
a.Tìm thiết diện của hình chóp S.ABCD với α . Thiết diện là hình gì?
b. Tính diện tích thiết diện theo a và x
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, cạnh a SA vuông góc với mặt phẳng (ABCD) và SA=a căn 2. Tính khoảng cách từ:
a) C đến mặt phẳng (SAB).
b) từ A đến (SCD).
c) Từ O đến (SCD).
d) Khoảng cách giữa hai đường thẳng AB và SC.
Cho hình chóp S.ABCD có đáy ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) . Hai điểm M và N lần lượt thay đổi trên hai cạnh CB và CD, đặt CM=x, CN=y, . Xác định hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SAN) vuông góc với nhau.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) . Hai điểm M và N lần lượt thay đổi trên hai cạnh CB và CD, đặt CM=x, CN=y, . Xác định hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SAN) vuông góc với nhau.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh 2a, SA vuông mặt phẳng (ABCD). SA bằng \(a\sqrt{3}\)
a) chứng minh (SCD) vuông góc với (SAD)
b) Xác định và tính góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD)
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) với SA = a√6.
a) Tính khoảng cách từ A và B đến mặt phẳng (SCD).
b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a 3 Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
A. 3 2
B. 14 4
C. 3 5
D. 22 5