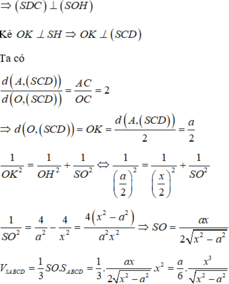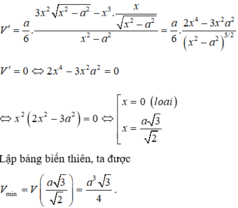Các câu hỏi tương tự
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến
S
C
D
bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V. A.
32
3
B.
8
3
C.
16
3
D.
16
3
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến S C D bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V.
A. 32 3
B. 8 3
C. 16 3
D. 16 3 3
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến
S
C
D
bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V A.
32
3
B.
8
3
C.
16
3
D.
16
3
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến S C D bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V
A. 32 3
B. 8 3
C. 16 3
D. 16 3 3
Cho hình chóp tứ giác đều S.ABCD đỉnh S , khoảng cách từ C đến mặt phẳng (SAB) bằng 6 . Gọi V là thể tích khối chóp S.ABCD, tính giá trị nhỏ nhất của V A.
18
3
B.
64
3
C.
27
3
D.
54
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD đỉnh S , khoảng cách từ C đến mặt phẳng (SAB) bằng 6 . Gọi V là thể tích khối chóp S.ABCD, tính giá trị nhỏ nhất của V
A. 18 3
B. 64 3
C. 27 3
D. 54 3
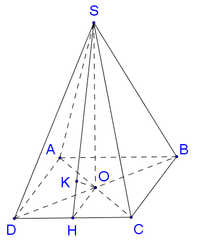
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ tâm O của đáy đến (SCD) bằng 2a, a là hằng số dương. Đặt ABx. Giá trị của x để thể tích của khối chóp SABCD đạt giá trị nhỏ nhất là A.
a
3
B.
2
a
6
C.
a
2
D.
a
6
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ tâm O của đáy đến (SCD) bằng 2a, a là hằng số dương. Đặt AB=x. Giá trị của x để thể tích của khối chóp SABCD đạt giá trị nhỏ nhất là
A. a 3
B. 2 a 6
C. a 2
D. a 6
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng
a
14
7
và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a. A.
V
3
a
3
2
2...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng a 14 7 và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a.
A. V = 3 a 3 2 2
B. V = 3 a 3 2 4
C. V = 3 a 3 2 16
D. V = 9 a 3 2 4
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng
a
3
2
6
.
Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC) A.
a
6
3
.
B.
a
6
3
.
C....
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng a 3 2 6 . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
A. a 6 3 .
B. a 6 3 .
C. a 6 6 .
D. a 6 .
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh
2
a
,
S
A
S
B
a
2
khoảng cách từ A đến mặt phẳng (SCD) bằng a. Thể tích của khối chóp đã cho bằng A.
2
a
3
3
3
B.
a...
Đọc tiếp
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 a , S A = S B = a 2 khoảng cách từ A đến mặt phẳng (SCD) bằng a. Thể tích của khối chóp đã cho bằng
A. 2 a 3 3 3
B. a 3 6 3
C. a 3 3 6
D. 2 a 3 6 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Biết rằng khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a. Xét góc α thảy đổi là số đo của góc giữa đường thẳng SB và mặt phẳng đáy. Tính
cos
α
sao cho thể tích của hình chóp S.ABCD đạt giá trị nhỏ nhất A.
cos
α
3
6
B.
cos
α
6
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Biết rằng khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a. Xét góc α thảy đổi là số đo của góc giữa đường thẳng SB và mặt phẳng đáy. Tính cos α sao cho thể tích của hình chóp S.ABCD đạt giá trị nhỏ nhất
A. cos α = 3 6
B. cos α = 6 3
C. cos α = 3 3
D. cos α = 6 6
Cho hình chóp S.ABCD có cạnh bên
S
A
a
0
a
3
và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD. A.
V
a
3
-
a
2
3
B. đ...
Đọc tiếp
Cho hình chóp S.ABCD có cạnh bên S A = a 0 < a < 3 và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
A. V = a 3 - a 2 3
B. đáp án khác
C. 2 2
D. 2