Ta vẽ hình như hình vẽ. E là trung điểm của CD, O H ⊥ S E .
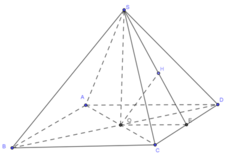
Dễ dàng cm được O H = d O ; S C D
= 1 2 d A ; S C D = 2
Gọi S E O ^ = α ( 0 < α < 90 0 )
⇒ O E = O H sin α = 2 sin α
S O = O H cos α = 2 cos α
⇒ Cạnh của hình vuông A B C D là : 4 sin α
Từ đó V S . A B C D = 1 3 S O . S A B C D = 32 3 . 1 sin 2 α . cos α .
Đặt cos α = t t ∈ 0 ; 1 thì sin 2 α . cos α = t 1 − t 2 .
Xét hàm f t = t − t 3 ; f ' t = 1 − 3 t 2 ; f ' t = 0 ⇔ t = − 1 3 t = 1 3
Ta có bảng biến thiên trên 0 ; 1
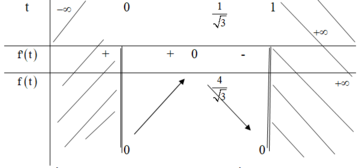
Vậy giá trị nhỏ nhất của V đạt được khi f t lớn nhất tức là min V = 16 3 .
Sửa lại đề bài thành giá trị nhỏ nhất



