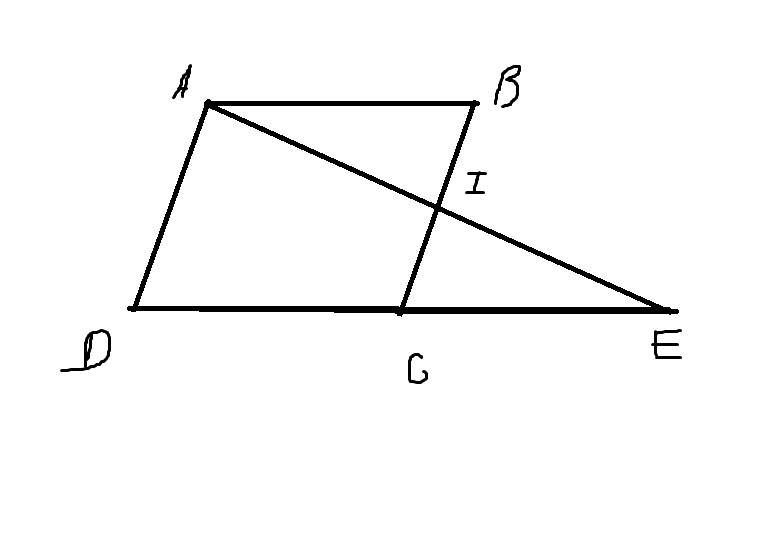
Xét tam giác AI B và tam giác EIC có:
\(\widehat{AIB}=\widehat{EIC}\) (đối đỉnh)
IC=IB( I trung điểm BC)
\(\widehat{ABI}=\widehat{ECI}\) (so le trong)
=> tam giác AIB= tam giác EIC (g.c.g)
=> IA=IE
Xét tứ giác ABEI có
2 đường chéo AE và BC cắt nhau tại trung điểm I của mỗi đường
=> tứ giác ABEI là hình bình hành
a, Xét tam giác CBA và tam giác ICE có
góc ABI = góc ICE ( do AB // CD - ABCD là hbh )
BI = IC ( do I là trung điểm BC)
góc AIB = góc EIC ( đối đỉnh)
=> 2 tam giác bằng nhau ( g-c-g)
=> AI = IE
Xét tứ giác ABEC có
I là trung điểm AE
I là trung điểm BC
=> ABEC là hình bình hành ( đpcm)
Xét tam giác CBA và tam giác ICE có
góc ABI = góc ICE ( do AB // CD - ABCD là hbh )
BI = IC ( do I là trung điểm BC)
góc AIB = góc EIC ( đối đỉnh)
=> 2 tam giác bằng nhau ( g-c-g)
=> AI = IE
Xét tứ giác ABEC có
I là trung điểm AE
I là trung điểm BC
=> ABEC là hình bình hành ( đpcm)
Xét tam giác CBA và tam giác ICE có
góc ABI = góc ICE ( do AB // CD )
BI = IC ( do I là trung điểm BC)
góc AIB = góc EIC ( đối đỉnh)
=> 2 tam giác bằng nhau ( g-c-g)
=> AI = IE
Xét tứ giác ABEC có
I là trung điểm AE
I là trung điểm BC
=> ABEC là hình bình hành ( đpcm)