Vì x>=0 nên miền nghiệm của bất phương trình x>=0 sẽ là nửa bên phải có chứa biên của đường thẳng Oy(1)
Vì y>=0 nên miền nghiệm của bất phương trình y>=0 sẽ là nửa bên trên có chứa biên của đường thẳng Ox(2)
Thay x=0 và y=0 vào x-y<=2, ta được:
0-0<=2
=>0<=2(đúng)
=>Miền nghiệm của bất phương trình x-y<=2 sẽ là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0) của đường thẳng x-y=2(3)
Thay x=0 và y=0 vào 2x+y<=7, ta được:
2*0+0<=7
=>0<=7(đúng)
=>Miền nghiệm của bất phương trình 2x+y<=7 sẽ là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0) của đường thẳng 2x+y<=7(4)
Từ (1),(2),(3),(4) ta có miền nghiệm của hệ bất phương trình sẽ là:
Theo hình, ta có miền nghiệm của hệ là tứ giác OABC, với O(0;0); A là giao điểm của trục Ox và đường thẳng x-y=2; B là giao điểm của hai đường thẳng x-y=2 và 2x+y=7; C là giao điểm của trục Oy và đường thẳng 2x+y=7
=>O(0;0); A(2;0); B(3;1); C(0;7)
Khi x=0 và y=0 thì T=2x+3y=0+0=0
Khi x=2 và y=0 thì T=2x+3y=4+0=4
Khi x=3 và y=1 thì T=2x+3y=6+3=9
Khi x=0 và y=7 thì T=2x+3y=0+21=21
Vậy: \(T_{\max}=21\) khi x=0 và y=7






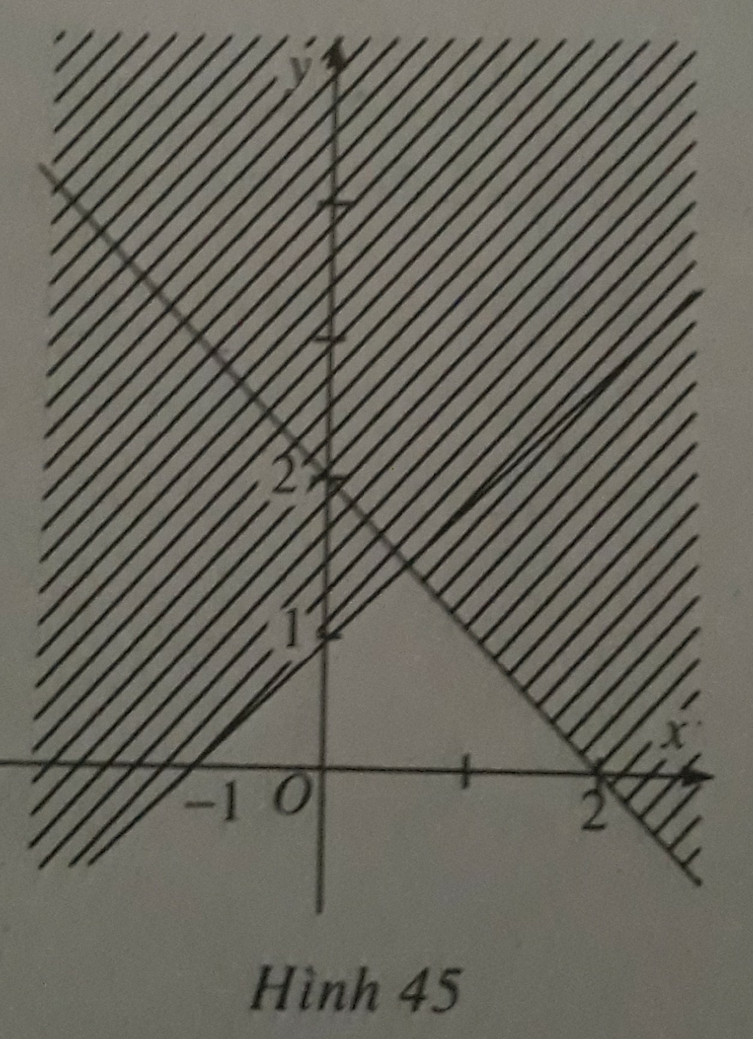
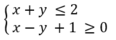 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.

