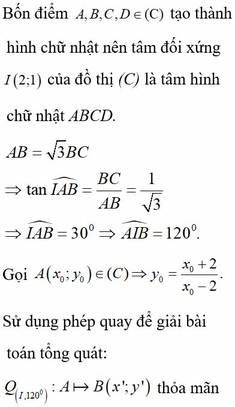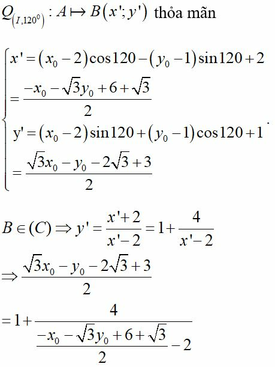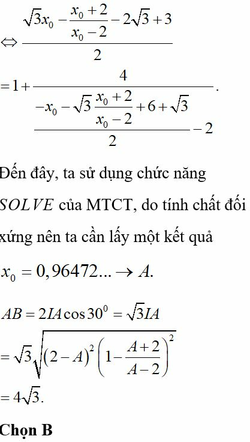Các câu hỏi tương tự
Cho đổ thị hàm số
y
x
+
1
x
-
1
có đổ thị như hình vẽ. Biết A, B, C, D thuộc đồ thị hàm số sao cho ABCD là hình chữ nhật có diện tích 6. Độ dài cạnh AB là A.
3
3
B.
3
C.
2
2
D.
2
Đọc tiếp
Cho đổ thị hàm số y = x + 1 x - 1 có đổ thị như hình vẽ. Biết A, B, C, D thuộc đồ thị hàm số sao cho ABCD là hình chữ nhật có diện tích 6. Độ dài cạnh AB là
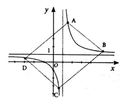
A. 3 3
B. 3
C. 2 2
D. 2
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
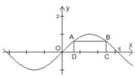
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hàm số
y
x
4
-
2
m
x
2
-
2
m
2
+
m
4
có đồ thị (C). Biết đồ thị (C )có ba điểm cực trị A, B, C và ABDC là hình thoi, trong đó D(0;-3), A thuộc trục tung. Khi đó m thuộc khoảng nào? A.
m
∈
(
9
/
5
;
2...
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 - 2 m 2 + m 4 có đồ thị (C). Biết đồ thị (C )có ba điểm cực trị A, B, C và ABDC là hình thoi, trong đó D(0;-3), A thuộc trục tung. Khi đó m thuộc khoảng nào?
A. m ∈ ( 9 / 5 ; 2 )
B. m ∈ ( - 1 ; 1 / 2 )
C. m ∈ ( 2 ; 3 )
D. m ∈ ( 1 / 2 ; 9 / 5 )
Cho hàm số
y
x
4
−
3
m
x
x
−
2
m
2
+
m
4
có đồ thị (C), biết đồ thị (C) có 3 điểm cực trị A, B, C và ABCD là hình thoi, trong đó
D
0
;
−
3
thuộc trục tung. Khi đó các giá trị của tham s...
Đọc tiếp
Cho hàm số y = x 4 − 3 m x x − 2 m 2 + m 4 có đồ thị (C), biết đồ thị (C) có 3 điểm cực trị A, B, C và ABCD là hình thoi, trong đó D 0 ; − 3 thuộc trục tung. Khi đó các giá trị của tham số m thuộc khoảng nào dưới đây?
A. m ∈ − 1 ; 1 2 .
B. m ∈ 2 ; 3 .
C. m ∈ 9 5 ; 2 .
D. m ∈ 1 2 ; 9 5 .
Cho hàm số
y
x
4
−
2
m
x
2
−
2
m
2
+
m
4
có đồ thị ( C). Biết đồ thị ( C) có ba điểm cực trị A, B, C và ABCD là hình thoi trong đó
D
0
;
−
3
,
A
thuộc trục tung. Khi đó m thuộc khoảng nào?...
Đọc tiếp
Cho hàm số y = x 4 − 2 m x 2 − 2 m 2 + m 4 có đồ thị ( C). Biết đồ thị ( C) có ba điểm cực trị A, B, C và ABCD là hình thoi trong đó D 0 ; − 3 , A thuộc trục tung. Khi đó m thuộc khoảng nào?
A. m ∈ − 1 ; 1 2
B. m ∈ 1 2 ; 9 5
C. m ∈ 9 5 ; 2
D. m ∈ 2 ; 3
Cho hai điểm A,B thuộc đồ thị hàm số ysinx trên đoạn
0
;
π
,
các điểm C,D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và
C
D
2
π
3
.Độ dài đoạn thẳng BC bằng A....
Đọc tiếp
Cho hai điểm A,B thuộc đồ thị hàm số y=sinx trên đoạn 0 ; π , các điểm C,D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và C D = 2 π 3 .
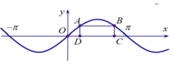
Độ dài đoạn thẳng BC bằng
A. 2 2 .
B. 1 2 .
C.1
D. 3 2 .
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a;b;c;d
∈
R, a
≠...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số
y
−
x
3
+
3
x
2
+
9
x
có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd. A. 144 B. 60 C. 180 D. 120
Đọc tiếp
Cho hàm số y = − x 3 + 3 x 2 + 9 x có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd.
A. 144
B. 60
C. 180
D. 120