a: f(x0)=x0+1
\(\lim\limits_{x\rightarrow x0}f\left(x\right)=x_0+1\)=f(x0)
=>HS f(x) liên tục tại điểm x0
b: Đồ thị hàm số là một đường thẳng liền mạch với mọi x thực
a: f(x0)=x0+1
\(\lim\limits_{x\rightarrow x0}f\left(x\right)=x_0+1\)=f(x0)
=>HS f(x) liên tục tại điểm x0
b: Đồ thị hàm số là một đường thẳng liền mạch với mọi x thực
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai .
I. Xét tính liên tục của hàm số f (x) =\(\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{x-1}|khix\ne1\\1-2x|khix=1\end{matrix}\right.\)tại điểm x0 = 1
II. Cho hàm số y = -x3 - x2 - 6x + 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C), biết rằng tiếp tuyến đó song song với đường thẳng
y = -6x + 17
III. Cho hình chóp S.ABCD có SA \(\perp\) (ABCD). Đáy ABCD là hình thang vuông tại A. Chứng minh rằng: BC \(\perp\) (SAB)
IV. Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a. AB vuông góc với mặt phẳng (BCD) và AB = \(\dfrac{a}{2}\). Tính khoảng cách từ D đến mp(ABC)
giải giúp mình nhé. cảm ơn các bạn
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
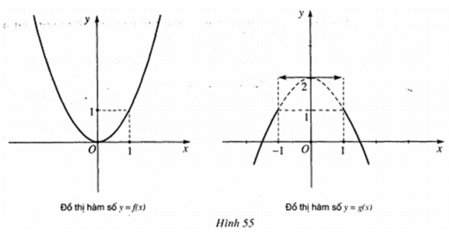
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
Cho hàm số y = f(x) xác định trên khoảng (a; b) chứa điểm x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) - f ( x 0 ) x - x 0 = L thì hàm số f(x) liên tục tại điểm x 0
Đặt g ( x ) = f ( x ) - f ( x 0 ) x - x 0 - L và biểu diễn f(x) qua g(x)
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Cho hàm số f(x) liên tục tại x 0 . Đạo hàm của f(x) tại x 0 là:
A. f x 0
B. f x 0 + h - f x 0 h
C. lim h → 0 f x 0 + h - f x 0 h (nếu tồn tại giới hạn)
D. lim h → 0 f x 0 + h - f x 0 - h h (nếu tồn tại giới hạn)