2.
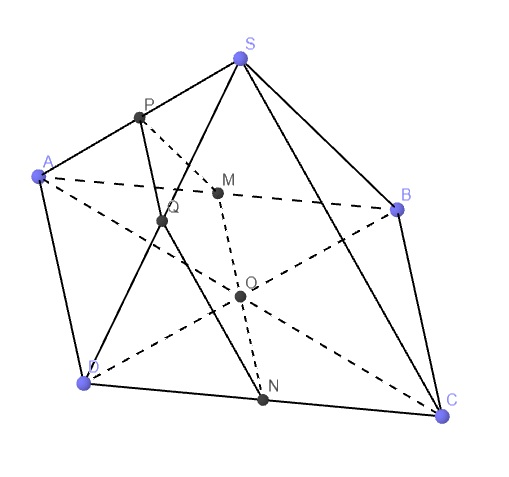
M là trung điểm AB, N là trung điểm CD nên MN là đường trung bình hbh ABCD
\(\Rightarrow MN||AD||BC\)
a. Đúng
\(\left\{{}\begin{matrix}MN||BC\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow MN||\left(SBC\right)\)
b. Đúng
Tương tự câu a
c. Sai
M là trung điểm AB, P là trung điểm SA nên MP là đường trung bình tam giác SAB
\(\Rightarrow MP||SB\Rightarrow SB||\left(MNP\right)\)
Do đó SB ko cắt (MNP)
d. Đúng
Qua P kẻ đường thẳng song song AD cắt SC tại Q
\(\left\{{}\begin{matrix}PQ||AD\Rightarrow PQ||MN\\P\in\left(MNP\right)\end{matrix}\right.\)
\(\Rightarrow PQ\in\left(MNP\right)\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SC\cap\left(MNP\right)\)
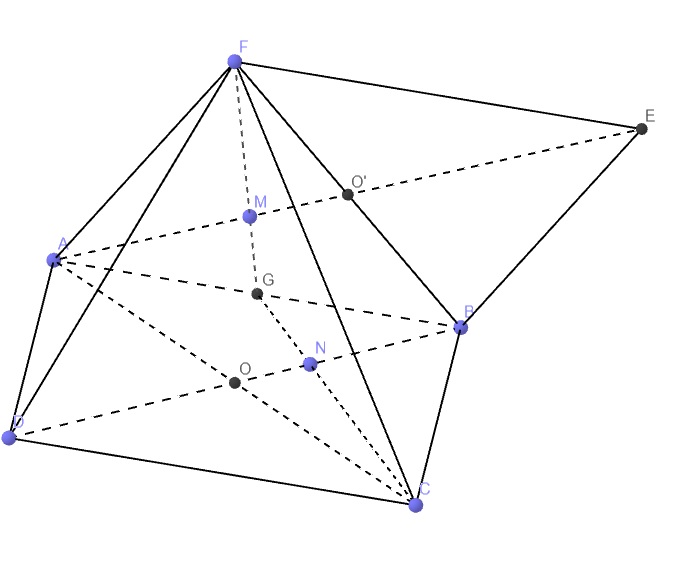
3.
a. Đúng
Do O là tâm hbh ABCD nên O là trung điểm BD
Do O' là tâm hbh ABEF nên O' là trung điểm BF
\(\Rightarrow OO'\) là đường trung bình tam giác BDF
\(\Rightarrow OO'||DF\)
Mà \(DF\in\left(ADF\right)\Rightarrow OO'||\left(ADF\right)\)
b. Sai
ABCD là hbh nên \(\left\{{}\begin{matrix}AB=CD\\AB||CD\end{matrix}\right.\)
ABEF là hbh nên \(\left\{{}\begin{matrix}AB=EF\\AB||EF\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}CD=EF\\CD||EF\end{matrix}\right.\) \(\Rightarrow CDFE\) là hbh
\(\Rightarrow CE||DF\)
Kết hợp câu a \(\Rightarrow OO'||CE\Rightarrow OO'||\left(BCE\right)\)
Do đó OO' ko cắt (BCE)
c. Sai
Ko hiểu câu này, hình như người ta đề nhầm lẫn, câu hỏi quá đơn giản vì đề bài cho sẵn \(BN=\dfrac{1}{3}BD\Rightarrow\dfrac{BN}{BD}=\dfrac{1}{3}\)
d. Đúng
Gọi G là trung điểm AB
Do O là trung điểm BD \(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{3}{2}.\dfrac{1}{3}BD=\dfrac{3}{2}BN\)
\(\Rightarrow\dfrac{BN}{BO}=\dfrac{2}{3}\)
Mà O là trung điểm BD \(\Rightarrow N\) là trọng tâm tam giác ABC
\(\Rightarrow N\) thuộc trung tuyến CG đồng thời \(\dfrac{GN}{GC}=\dfrac{1}{3}\) theo t/c trung tuyến
Tương tự ta có M là trọng tâm tam giác ABF \(\Rightarrow\left\{{}\begin{matrix}M\in GF\\\dfrac{GM}{GF}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\dfrac{GN}{GC}=\dfrac{GM}{GF}=\dfrac{1}{3}\Rightarrow MN||CF\) theo định lý Thales đảo
\(\Rightarrow MN||\left(CDFE\right)\)