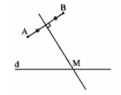
Ta có \(\left|MA-MB\right|\ge0\) với một điểm M tùy ý và \(\left|MA-MB\right|=0\) chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB.
Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d.
Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì \(\left|MA-MB\right|\) đạt giá trị nhỏ nhất và bằng 0.
Ta có `:|MA-MB|>=0` với `1` điểm `M` tuỳ ý và `|MA-MB|=0` chỉ với các điểm `M` mà `MA=MB` , tức là chỉ với các điểm `M` nằm trên đg trung trực đoạn thẳng `AB`
Mặt khác , `M in d` . Vậy `M ` là giao điểm của đg thẳng `d` và đg trung trực của đoạn thẳng `AB` . Có giao điểm này vì `AB` không vuông góc với `d`
Tóm lại : Khi `M` là giao điểm của `d` và đg trung trực của `AB` thì `|MA-MB|` đạt giá trị nhỏ nhất và `=0`
Tham khảo:
https://hoc24.vn/cau-hoi/cho-duong-thang-d-va-hai-diem-a-b-nam-ve-mot-phia-cua-d-sao-cho-ab-khong-vuong-goc-voi-d-hay-tim-tren-d-mot-diem-m-sao-cho-leftma-mbright-co.157927030573
Ta có :|MA−MB|≥0:|MA-MB|≥0 với 11 điểm MM tuỳ ý và |MA−MB|=0|MA-MB|=0 chỉ với các điểm MM mà MA=MBMA=MB , tức là chỉ với các điểm MM nằm trên đg trung trực đoạn thẳng ABAB
Mặt khác , M∈dM∈d . Vậy MM là giao điểm của đg thẳng dd và đg trung trực của đoạn thẳng ABAB . Có giao điểm này vì ABAB không vuông góc với dd
Tóm lại : Khi MM là giao điểm của dd và đg trung trực của ABAB thì |MA−MB||MA-MB| đạt giá trị nhỏ nhất và =0=0
Ta có |MA−MB|≥0|MA−MB|≥0 với một điểm M tùy ý và |MA−MB|=0|MA−MB|=0 chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB.
Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d.
Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì |MA−MB||MA−MB| đạt giá trị nhỏ nhất và bằng 0.